题目内容
【题目】已知Rt△ABC,AB=3,BC=4,CA=5,P为△ABC外接圆上的一动点,且 ![]() 的最大值是( )
的最大值是( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】B
【解析】解:以AC的中点为原点,以ACx轴,建立如图所示的平面直角坐标系,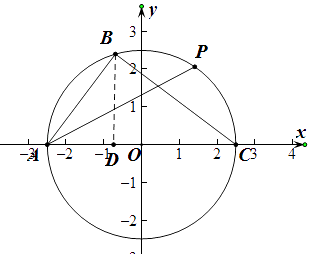
则△ABC外接圆的方程为x2+y2=2.52 ,
设P的坐标为( ![]() cosθ,
cosθ, ![]() sinθ),
sinθ),
过点B作BD垂直x轴,
∵sinA= ![]() ,AB=3
,AB=3
∴BD=ABsinA= ![]() ,AD=ABcosA=
,AD=ABcosA= ![]() ×3=
×3= ![]() ,
,
∴OD=AO﹣AD=2.5﹣ ![]() =
= ![]() ,
,
∴B(﹣ ![]() ,
, ![]() ),
),
∵A(﹣ ![]() ,0),C(
,0),C( ![]() ,0)
,0)
∴ ![]() =(
=( ![]() ,
, ![]() ),
), ![]() =(5,0),
=(5,0), ![]() =(
=( ![]() cosθ+
cosθ+ ![]() ,
, ![]() sinθ)
sinθ)
∵ ![]() =x
=x ![]() +y
+y ![]()
∴( ![]() cosθ+
cosθ+ ![]() ,
, ![]() sinθ)=x(
sinθ)=x( ![]() ,
, ![]() )+y(5,0)=(
)+y(5,0)=( ![]() x+5y,
x+5y, ![]() x)
x)
∴ ![]() cosθ+
cosθ+ ![]() =
= ![]() x+5y,
x+5y, ![]() sinθ=
sinθ= ![]() x,
x,
∴y= ![]() cosθ﹣
cosθ﹣ ![]() sinθ+
sinθ+ ![]() ,x=
,x= ![]() sinθ,
sinθ,
∴x+y= ![]() cosθ+
cosθ+ ![]() sinθ+
sinθ+ ![]() =
= ![]() sin(θ+φ)+
sin(θ+φ)+ ![]() ,其中sinφ=
,其中sinφ= ![]() ,cosφ=
,cosφ= ![]() ,
,
当sin(θ+φ)=1时,x+y有最大值,最大值为 ![]() +
+ ![]() =
= ![]() ,
,
故选:B
【考点精析】解答此题的关键在于理解平面向量的基本定理及其意义的相关知识,掌握如果![]() 、
、![]() 是同一平面内的两个不共线向量,那么对于这一平面内的任意向量
是同一平面内的两个不共线向量,那么对于这一平面内的任意向量![]() ,有且只有一对实数
,有且只有一对实数![]() 、
、![]() ,使
,使![]() .
.

练习册系列答案
相关题目