题目内容
CD是△ABC中AB边上的高,已知CD=6,DA=3,DB=12,则
- A.CA2+BC2=AB2
- B.∠CAB=∠CBD
- C.∠CAB>∠ACB
- D.∠ACD=∠BCD
A
分析:画出图形,根据CD、DA计算AC,根据DB、DA计算AB,解直角△ACD、直角△CBD则可得A选项正确.
解答: 解:CA2+BC2=AD2+CD2+BD2+CD2=144+36+36+9=225,
解:CA2+BC2=AD2+CD2+BD2+CD2=144+36+36+9=225,
AB=DA+DB=15,AB2=225,
∴CA2+BC2=AB2=225,(A选项正确)
且AD=3,CD=6,BD=12,CD⊥AB,
∴△BCD∽△CAD,
∠ACD=∠CBD,∠BCD=∠CAD,(故B、D选项错误),
在△ABC中,AB>BC,
∠CAB<∠ACB,(故C选项错误).
故选A.
点评:本题考查了勾股定理在直角三角形中的运用,本题中正确的求AC.BC的长度是解本题的关键.
分析:画出图形,根据CD、DA计算AC,根据DB、DA计算AB,解直角△ACD、直角△CBD则可得A选项正确.
解答:
 解:CA2+BC2=AD2+CD2+BD2+CD2=144+36+36+9=225,
解:CA2+BC2=AD2+CD2+BD2+CD2=144+36+36+9=225,AB=DA+DB=15,AB2=225,
∴CA2+BC2=AB2=225,(A选项正确)
且AD=3,CD=6,BD=12,CD⊥AB,
∴△BCD∽△CAD,
∠ACD=∠CBD,∠BCD=∠CAD,(故B、D选项错误),
在△ABC中,AB>BC,
∠CAB<∠ACB,(故C选项错误).
故选A.
点评:本题考查了勾股定理在直角三角形中的运用,本题中正确的求AC.BC的长度是解本题的关键.

练习册系列答案
相关题目
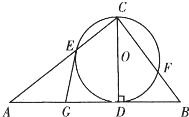 如图,已知CD是△ABC中AB边上的高,以CD为直径的⊙O分别交CA,CB于点E,F,点G是AD的中点.求证:GE是⊙O的切线.
如图,已知CD是△ABC中AB边上的高,以CD为直径的⊙O分别交CA,CB于点E,F,点G是AD的中点.求证:GE是⊙O的切线.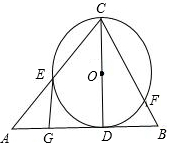 如图,已知CD是△ABC中AB边上的高,以CD为直径的⊙O交CA于点E,点G是AD的中点.
如图,已知CD是△ABC中AB边上的高,以CD为直径的⊙O交CA于点E,点G是AD的中点.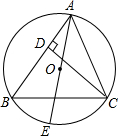 已知:如图,△ABC内接于⊙O,AE是⊙O的直径,CD是△ABC中AB边上的高,
已知:如图,△ABC内接于⊙O,AE是⊙O的直径,CD是△ABC中AB边上的高, 已知CD是△ABC中AB边上的高,AC+BC=8,CD=2,AE是△ABC的外接圆的直径,
已知CD是△ABC中AB边上的高,AC+BC=8,CD=2,AE是△ABC的外接圆的直径,