题目内容
如图所示，P是边长为8的正方形ABCD形外一点，PB=PC，△PBD的面积等于48，求△PBC的面积．
解：设PD与BC交点是O，取BC中点E，连接PE．
∵PB=PC，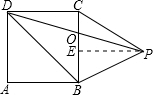
∴PE⊥BC，
∵四边形ABCD是正方形，
∴CD⊥BC，
∴PE∥CD．
设PE=x，
∴
，
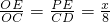∵OE+OC=CE=
BC=4，
∴OE=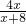
，
∴OB=OE+BE=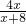+4=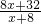
，
∴S△PBD=S△PBO+S△DBO=BO•PE+BO•DC=（PE+DC）BO=（x+8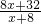）•=4x+16=48，
∴x=8，
∴PE=8，
∴S△PBC=PE•BC=×8×8=32．
分析：首先设PD与BC交点是O，取BC中点E，连接PE，根据等腰三角形与正方形的性质，可得PE∥CD，然后设PE=x，根据平行线分线段成比例定理，即可求得OB的长，又由S△PBD=S△PBO+S△DBO=48，即可求得x的值，继而求得△PBC的面积．
点评：此题考查了正方形的性质，等腰三角形的性质，平行线分线段成比例定理等知识．此题难度较大，解题的关键是注意数形结合思想与方程思想的应用，注意辅助线的作法．
∵PB=PC，
∴PE⊥BC，
∵四边形ABCD是正方形，
∴CD⊥BC，
∴PE∥CD．
设PE=x，
∴
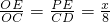，∵OE+OC=CE=
BC=4，∴OE=
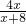，∴OB=OE+BE=
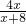+4=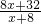，∴S△PBD=S△PBO+S△DBO=
BO•PE+BO•DC=（PE+DC）BO=（x+8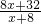）•=4x+16=48，∴x=8，
∴PE=8，
∴S△PBC=
PE•BC=×8×8=32．分析：首先设PD与BC交点是O，取BC中点E，连接PE，根据等腰三角形与正方形的性质，可得PE∥CD，然后设PE=x，根据平行线分线段成比例定理，即可求得OB的长，又由S△PBD=S△PBO+S△DBO=48，即可求得x的值，继而求得△PBC的面积．
点评：此题考查了正方形的性质，等腰三角形的性质，平行线分线段成比例定理等知识．此题难度较大，解题的关键是注意数形结合思想与方程思想的应用，注意辅助线的作法．
练习册系列答案
相关题目
如图所示，△ABC是边长为6cm的等边三角形，被一平行于BC的矩形所截，AB被截成三等分，则图中阴影部分的面积为
如图所示，P是边长为1的正三角形ABC的BC边上一点，从P向AB作垂线PQ，Q为垂足．延长QP与AC的延长线交于R，设BP=x（0≤x≤1），△BPQ与△CPR的面积之和为y，把y表示为x的函数是
（2013•泰州一模）一个包装盒的设计方法如图所示，ABCD是边长为60cm的正方形硬纸片，切去阴影部分所示的四个全等的等腰直角三角形，再沿虚线折起，使得ABCD四个点重合于图中的点P，正好形成一个正四棱柱形状的包装盒，E、F在AB上是被切去的等腰直角三角形斜边的两个端点，设AE=FB=xcm．若广告商要求包装盒侧面积S（cm2）最大，试问x应取的值为
如图所示，△OAB是边长为