题目内容
如图，已知△ABC为等边三角形，点D、E分别在BC、AC边上，AD与BE相交于点F，且AE=CD，．
（1）求证：AD=BE；
（2）求∠BFD的度数．
（1）证明：∵AB=AC，AE=CD，∠BAE=∠C=60°，
在△ABE和△ACD中，
，
∴△ABE≌△ACD（SAS），
∴AD=BE．
（2）解：∵△ABE≌△ACD，
∴∠ABE=∠CAD，
∴∠BFD=∠ABE+∠BAP=∠CAD+∠BAP=∠BAC=60°．
分析：（1）SAS可得△ABE≌△ACD，进而得出对应边相等．
（2）根据全等三角形的性质推出∠ABE=∠CAD再通过角之间的转化即可求解∠BFD的度数．
点评：主要考查了等边三角形的性质以及全等三角形的判定及性质问题，应熟练掌握并能进行一些简单的计算问题．
在△ABE和△ACD中，
，∴△ABE≌△ACD（SAS），
∴AD=BE．
（2）解：∵△ABE≌△ACD，
∴∠ABE=∠CAD，
∴∠BFD=∠ABE+∠BAP=∠CAD+∠BAP=∠BAC=60°．
分析：（1）SAS可得△ABE≌△ACD，进而得出对应边相等．
（2）根据全等三角形的性质推出∠ABE=∠CAD再通过角之间的转化即可求解∠BFD的度数．
点评：主要考查了等边三角形的性质以及全等三角形的判定及性质问题，应熟练掌握并能进行一些简单的计算问题．
练习册系列答案
名校课堂系列答案
相关题目
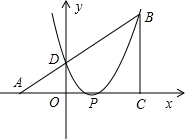，m）（m＞0），线段AB与y轴相交于点D，以P（1，0）为顶点的二次函数图象经过点B、D．
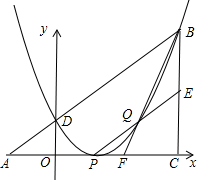如图，已知△ABC为直角三角形，∠ACB=90°，AC=BC，点A、C在x轴上，点B坐标为（3，m）（m＞0），线段AB与y轴相交于点D，以P（1，0）为顶点的抛物线过点B、D．
25、如图，已知△ABC为等边三角形，D、F分别为BC、AB边上的点，CD=BF，以AD为边作等边△ADE．
如图，已知△ABC为等边三角形，D，E，F分别在边BC，CA，AB上，且△DEF也是等边三角形，除已知相等的边以外，请你猜想还有哪些相等线段，并证明你的猜想是正确的．
如图，已知△ABC为等边三角形，点D．E分别在BC．AC边上，且AE=CD，AD与BE相交于点F．