Question

如图，已知⊙C经过原点O，并与两坐标轴交于A、D两点，点B在⊙C上，∠OBA=30°，点D的坐标为（0，6）．
求：（1）点A的坐标；
（2）圆心C的坐标；
（3）⊙C的面积．

Answer 1

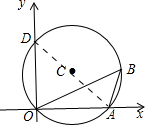解：连接AD，∵∠DOA=90°，
∴AD为直径，即点C在AD上，
由圆周角定理，得∠D=∠OBA=30°，
在Rt△OAD中，OD=6，则OA=2，AD=4，
即圆的半径为2．
（1）因为OA=2，所以点A的坐标为（2，0）；
（2）点C为AD的中点，故圆心C的坐标为（，3）；
（3）因为圆的半径为2，所以⊙C的面积为π（2）²=12π平方单位．
分析：根据直角坐标系的两坐标轴的垂直关系，连接AD，可证AD为直径；将已知圆周角∠OBA转化，即∠D=∠OBA=30°，在Rt△OAD中，解答本题的几个问题．
点评：充分发挥辅助线AD的作用，将已知条件集中到Rt△OAD中解直角三角形．