Question

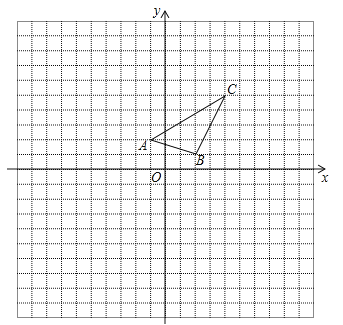
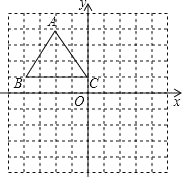
【题目】如图，在平面直角坐标系中，△ABC三个顶点的坐标分别为A（﹣2，4），B（﹣4，1），C（0，1）．

（1）画出与△ABC关于x轴对称的△A1B1C1，并写出点C1的坐标；

（2）画出以C1为旋转中心，将△A1B1C1逆时针旋转90°后的△A2B2C2；

（3）尺规作图：连接A1A2，在C1A2边上求作一点P，使得点P到A1A2的距离等于PC1的长（保留作图痕迹，不写作法）；

（4）请直接写出∠C1A1P的度数．

Answer 1

【答案】（1）C1（0，﹣1）；图见解析；（2）见解析；（3）见解析；（4）22.5°.

【解析】

（1）分别作出A、B、C三点关于x轴的对称点A1、B1、C1即可；

（2）分别作出A1、B1、C1的对应点A2、B2、C2即可；

（3）作∠C1A1A2的角平分线交C1A2于P即可；

（4）根据角平分线的定义即可解决问题；

解：（1）△A1B1C1如图所示，并写出点C1的坐标（0，﹣1）；

（2）△A2B2C2如图所示；

（3）点P如图所示；

（4）请直接写出∠C1A1P的度数为22.5°；