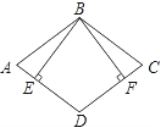
题目内容
如图,四边形ABCD是菱形,BE⊥AD、BF⊥CD,垂足分别为E、F.
(1)求证:BE=BF;
(2)当菱形ABCD的对角线AC=8,BD=6时,求BE的长.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
如图,四边形ABCD是菱形,BE⊥AD、BF⊥CD,垂足分别为E、F.
(1)求证:BE=BF;
(2)当菱形ABCD的对角线AC=8,BD=6时,求BE的长.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案