Question

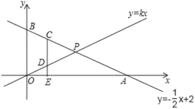
【题目】在平面直角坐标系中，一次函数的图象交轴、轴分别于两点，交直线于。

（1）求点的坐标；

（2）若，求的值；

（3）在（2）的条件下，是线段上一点，轴于，交于，若，求点的坐标。

Answer 1

【答案】（1），；（2）；（3）点的坐标为.

【解析】

(1)分别代入x=0、y=0求出y、x的值，由此可得出点B. A的坐标；

(2)设点P的坐标为(x,y)，利用一次函数图象上点的坐标特征结合等腰三角形的性质可得出点P的坐标，再由点P在直线y=kx上利用一次函数图象上点的坐标特征可求出k值；

(3)设点C的坐标为(x, x+2)，则点D的坐标为(x,x)，点E的坐标为(x,0)，进而可得出CD、DE的长度，由CD=2DE可得出关于x的一元一次方程，解之即可得出结论

解：（1）当时，，

当时，，

，

；

（2）设，因为点在直线，且,

，

把代入，所以点的坐标是，

因为点在直线上，所以；

（3）设点，则，，

因为，，

解得：，则，

所以点的坐标为.