题目内容
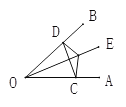
【题目】如图1,已知函数![]() 与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.
与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.

(1)求直线BC的函数解析式;
(2)设点M是x轴上的一个动点,过点M作y轴的平行线,交直线AB于点P,交直线BC于点Q.
①若△PQB的面积为![]() ,求点M的坐标;
,求点M的坐标;
②连接BM,如图2,若∠BMP=∠BAC,求点P的坐标.
【答案】(1)![]() ;(2)①M(
;(2)①M(![]() ,0)或(
,0)或(![]() ,0);②P(
,0);②P(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
(1)先根据坐标轴上点的特征求出A、B的坐标,进而求得点C的坐标,最后用待定系数法即可得出结论;
(2) ①设点M的坐标,进而得到点P、Q的坐标,得到PQ长,最后用面积公式即可得出结论;
②利用点C与点A关于y轴对称,QM![]() 轴,证得
轴,证得![]() ;设出M的坐标,利用勾股定理建立方程求解,得到点P的坐标;根据直线BA和BC关于y轴对称,即可求得点P关于y轴对称的另一个点的坐标.
;设出M的坐标,利用勾股定理建立方程求解,得到点P的坐标;根据直线BA和BC关于y轴对称,即可求得点P关于y轴对称的另一个点的坐标.
(1)对于函数![]()
令![]() ,则
,则![]() ;令
;令![]() ,则
,则![]() ;
;
∴直线![]() 与坐标轴的交点坐标为:A(-6,0),B(0,3)
与坐标轴的交点坐标为:A(-6,0),B(0,3)
∵点C与点A关于y轴对称
∴点C的坐标为(6,0)
设直线BC的函数解析式为:![]()
将C (6,0)代入得:![]()
解得:![]()
∴直线BC的函数解析式为:![]()
(2) ①设点M的坐标为(n,0)
∵点P在直线![]() 上,∴点P的坐标为(
上,∴点P的坐标为(![]() ,
,![]() )
)
∵点![]() 在直线
在直线![]() 上,∴点
上,∴点![]() 的坐标为(
的坐标为(![]() ,
,![]() )
)
∴![]()
∵△PQB的面积为![]() ,
,
∴![]()
解得:![]()
∴M(![]() ,0)或(
,0)或(![]() ,0);
,0);
②∵点C与点A关于y轴对称,∴![]() ,
,
∵QM![]() 轴,∴
轴,∴![]() ,
,
∵∠BMP=∠BAC,∴![]() ,
,
∵![]() ,∴
,∴![]()
设点M的坐标为![]() ,则点P的坐标为(
,则点P的坐标为(![]() ,
,![]() )
)
∵![]()
在![]() 中,
中,
![]()
![]()
![]()
∴![]()
∴![]()
解得:![]() ,
,
∴点P的坐标为:(![]() ,
,![]() )
)
∵直线BA和BC关于y轴对称,
∴点P关于y轴的对称点为:(![]() ,
,![]() )
)
故点P的坐标为:(![]() ,
,![]() )或(
)或(![]() ,
,![]() )
)

练习册系列答案
相关题目