题目内容
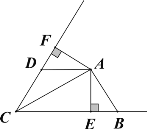
【题目】如图,![]() 中,点
中,点![]() 是边
是边![]() 上一个动点,过
上一个动点,过![]() 作直线
作直线![]() ,设
,设![]() 交
交![]() 的平分线于点
的平分线于点![]() ,交
,交![]() 的外角平分线于点
的外角平分线于点![]() .
.
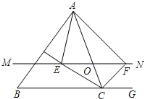
![]() 求证:
求证:![]() ;
;
![]() 当点
当点![]() 在
在![]() 上运动到何处时,四边形
上运动到何处时,四边形![]() 为矩形?请说明理由;
为矩形?请说明理由;
![]() 当点
当点![]() 在
在![]() 上运动时,四边形
上运动时,四边形![]() 能为菱形吗?请说明理由.
能为菱形吗?请说明理由.
【答案】(1)见解析;(2)当点![]() 在边
在边![]() 上运动到
上运动到![]() 中点时,四边形
中点时,四边形![]() 是矩形,理由见解析;(3)不可能,理由见解析
是矩形,理由见解析;(3)不可能,理由见解析
【解析】
(1)由直线MN∥BC,MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F,易证得OE=OC,同理可证OC=OF,则可证得OE=OF=OC;
(2)根据平行四边形的判定以及矩形的判定得出即可.
(3)菱形的判定问题,若使菱形,则必有四条边相等,对角线互相垂直,进而分析求出即可.
![]() 证明:∵
证明:∵![]() 是
是![]() 的平分线,
的平分线,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
同理可证![]() ,
,
∴![]() ;
;![]() 解:当点
解:当点![]() 在边
在边![]() 上运动到
上运动到![]() 中点时,四边形
中点时,四边形![]() 是矩形.
是矩形.
理由是:当![]() 为
为![]() 的中点时,
的中点时,![]() ,
,
∵![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∵![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,
∴![]() ,
,

∴平行四边形![]() 是矩形.
是矩形.![]() 解:不可能.
解:不可能.
理由如下:如图,连接![]() ,
,
∵![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,
∴![]() ,
,
若四边形![]() 是菱形,则
是菱形,则![]() ,
,
但在![]() 中,不可能存在两个角为
中,不可能存在两个角为![]() ,所以不存在其为菱形.
,所以不存在其为菱形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目