题目内容
如图，直线l1：y1=k1x+b1与直线l2：y2=k2x+b2的交点坐标是（2，-1），那么当y1＜y2时，x的取值范围是________．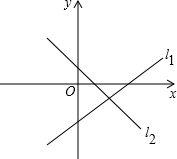
x＜2
分析：在图中找到两函数图象的交点，根据一次函数图象的交点坐标与不等式组解集的关系即可作出判断．
解答：∵直线l1：y1=k1x+b1与直线l2：y2=k2x+b2的交点坐标是（2，-1），
∴当x=2时，y1=y2=-1；
而当y1＜y2时，x＜2．
故答案为x＜2．
点评：此题考查了直线交点坐标与一次函数组成的不等式组的解的关系，利用图象即可直接解答，体现了数形结合思想在解题中的应用．
分析：在图中找到两函数图象的交点，根据一次函数图象的交点坐标与不等式组解集的关系即可作出判断．
解答：∵直线l1：y1=k1x+b1与直线l2：y2=k2x+b2的交点坐标是（2，-1），
∴当x=2时，y1=y2=-1；
而当y1＜y2时，x＜2．
故答案为x＜2．
点评：此题考查了直线交点坐标与一次函数组成的不等式组的解的关系，利用图象即可直接解答，体现了数形结合思想在解题中的应用．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
8、如图，直线l1：y1=k1x+b1与直线l2：y2=k2x+b2的交点坐标是（2，-l），那么当y1＜y2时，x的取值范围是
已知：如图，直线l1：y1=a1x-b1与直线l2：y2=a2x-b2相交于点P（-1，2），则方程组的
（2013•盐城模拟）如图，直线l1：y1=x+1与直线l2：y2=mx+n相交于点P（1，b）．当y1＞y2时，x的取值范围为
-2，0），与y轴交于点C．两条直线相交于点D，连接AB．
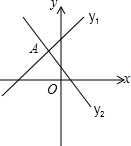如图，直线l1：y1=k1x+b1与直线l2：y2=k2x+b2的交点为（-1，2）．当函数值y1＞y2时，自变量x的取值范围为（ ）| A、等于-1 | B、小于-1 | C、大于-1 | D、以上都不对 |