题目内容
 在平面直角坐标系中有四点,其中三点坐标分别为A(-2,1),B(-3,-1),C(1,-1).若以A、B、C、D为顶点的四边形是平行四边形,那么点D的坐标不可能是
在平面直角坐标系中有四点,其中三点坐标分别为A(-2,1),B(-3,-1),C(1,-1).若以A、B、C、D为顶点的四边形是平行四边形,那么点D的坐标不可能是
- A.(2,1)
- B.(-6,1)
- C.(1,-3)
- D.(0,-3)
C
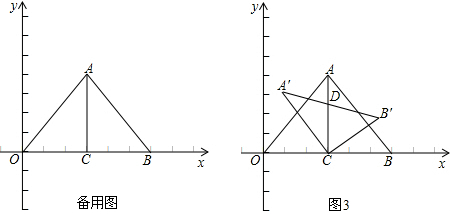
分析:根据平行四边形的性质可知,平行四边形的对比平行且相等,故连接各个顶点,数形结合,可以作出D点可能的位置,故可以确定D点可能的坐标,利用排除法,确定答案.
解答:如图:
∴点D的坐标可能为(2,1),(-6,1),(0,3).

故选C.
点评:此题考查了平行四边形的性质:平行四边形的对边平行且相等.解此题的关键是注意数形结合思想的应用.
分析:根据平行四边形的性质可知,平行四边形的对比平行且相等,故连接各个顶点,数形结合,可以作出D点可能的位置,故可以确定D点可能的坐标,利用排除法,确定答案.
解答:如图:
∴点D的坐标可能为(2,1),(-6,1),(0,3).

故选C.
点评:此题考查了平行四边形的性质:平行四边形的对边平行且相等.解此题的关键是注意数形结合思想的应用.

练习册系列答案
相关题目
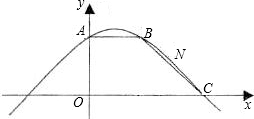 在x轴上,过A、B、C三点的抛物线表达式为
在x轴上,过A、B、C三点的抛物线表达式为