Question

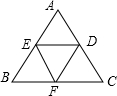△ABC是等边三角形，D，E，F为各边中点，则图中共有正三角形

1. A.
   2个
2. B.
   3个
3. C.
   4个
4. D.
   5个

Answer 1

D
分析：根据等边三角形的判定方法，可知三边，三内角相等的三角形为等边三角形，由AB=BC=AC，且D，E，F为各边中点，可知：AE=EB=BF=FC=CD=DA=DE=EF=FD．所以图中三角形均为等边三角形．
解答：因为△ABC为等边三角形，所以AB=BC=AC，
又因为D，E，F为各边中点，所以AE=EB=BF=FC=CD=DA；
又因为DE，DF，EF分别为中位线，所以DE=BC，EF=AC，DF=AB，
即DE=EF=DF．所以AE=EB=BF=FC=CD=DA=DE=EF=FD．
所以此图中所有的三角形均为等边三角形．
因此应选择5个，
故选择D．
点评：考查中位线定理，以及中点的应用．三角形判定方法，即三边相等的三角形均为等边三角形．