题目内容
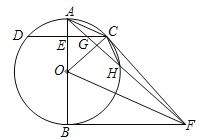
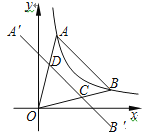
【题目】如图,点A,B在反比例函数y=![]() (x >0)的图象上,点A在点B的左侧,且OA=OB,点A关于y轴的对称点为A′,点B关于x轴的对称点为B′,连接A′B′ 分别交OA,OB于点D,C,若四边形ABCD的面积为
(x >0)的图象上,点A在点B的左侧,且OA=OB,点A关于y轴的对称点为A′,点B关于x轴的对称点为B′,连接A′B′ 分别交OA,OB于点D,C,若四边形ABCD的面积为![]() ,则点A的坐标为_______.
,则点A的坐标为_______.
【答案】(![]() ,2)
,2)
【解析】∵反比例函数y= ![]() ,关于直线y=x对称, OA=OB,
,关于直线y=x对称, OA=OB,
∴A、B关于直线y=x对称,
设点A的坐标为(m, ![]() ),则点B的坐标为(
),则点B的坐标为( ![]() ,m),则点A′的坐标为(-m,
,m),则点A′的坐标为(-m, ![]() ),点B′的坐标为(
),点B′的坐标为(![]() ,-m),
,-m),
∴直线OB的解析式为y=m2x, 直线A′B′的解析式为y=-x+![]() -m,
-m,
由 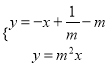 ,解得
,解得 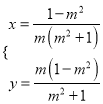
∴C[ 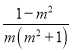 ,
, ![]() ],根据对称性可知D[
],根据对称性可知D[ ![]() ,
, 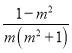 ],
],
如图,设A′B′交x轴于F,交y轴于E,连接AA′,作DN⊥OF于N,CM⊥OE于M,DN交CM于G.
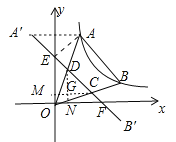
∵OE=OF= ![]() -m,
-m,
∴∠OEF=∠OFE=45°,
∴∠A′EA=90°,AE=![]() m,
m,
在Rt△CDG中,∵DG=CG,CD= ![]() CG=
CG= ![]() [
[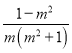 -
-![]() ].
].
同理可得,AB= ![]() (
(![]() -m),
-m),
∵四边形![]() ,
,
∴ 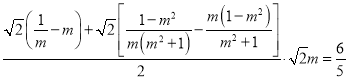
整理得![]() ,解得
,解得![]() ,∵m>0,
,∵m>0,
∴m=![]() ,
,
∴A( ![]() ,2).
,2).

练习册系列答案
相关题目