题目内容
【题目】如图,已知∠ACB=∠DCE=90°,AC=BC=6,CD=CE,AE=3,∠CAE=45°,求AD的长.
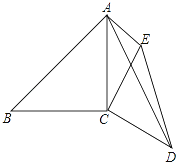
【答案】AD=9.
【解析】
连接BE,根据已知条件先证出∠BCE=∠ACD,根据SAS证出△ACD≌△BCE,得出AD=BE,再根据勾股定理求出AB,然后根据∠BAC=∠CAE=45°,求出∠BAE=90°,在Rt△BAE中,根据AB、AE的值,求出BE,从而得出AD.
如图,连接BE,

∵∠ACB=∠DCE=90°,∴∠ACB+∠ACE=∠DCE+∠ACE,
即∠BCE=∠ACD,
又∵AC=BC,DC=EC,
在△ACD和△BCE中,
 ,
,
∴△ACD≌△BCE(SAS),
∴AD=BE,
∵AC=BC=6,∴AB=6 ,
∵∠BAC=∠CAE=45°,∴∠BAE=90°,
在Rt△BAE中,AB=6![]() ,AE=3,
,AE=3,
∴BE=![]() =
=![]() =
=![]() =9,
=9,
∴AD=9.

练习册系列答案
相关题目








