Question

如图，直线由直线：沿轴向右平移9个单位得到，则直线与直线的距离为          ．

Answer 1

 

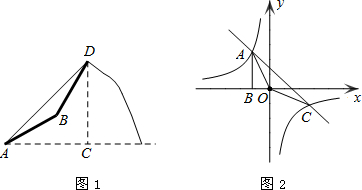
解析试题分析：直线a、b分别与x轴交于A、B，过B点作BC⊥直线a，CD⊥AB于D点，先确定A点坐标为（-3，0），根据平移确定B点坐标为（6，0），设C点坐标为（m，n），则n=m+4，易得△ADC∽△CDB，则CD：DB=AD：DB，即CD²=AD•DB，于是（m+4）²=（m+3）（6-m），解得m₁=，m₂=-3（舍去），然后计算出BD与CD的值，再利用勾股定理计算BC即可．
直线a、b分别与x轴交于A、B，过B点作BC⊥直线a，CD⊥AB于D点

把x=0代入y=x+4得x+4=0，解得x=-3，则A点坐标为（-3，0），
∵直线b由直线a：y=x+4沿x轴向右平移9个单位得到，
∴B点坐标为（6，0），
设C点坐标为（m，n），则n=m+4，
∵△ADC∽△CDB，
∴CD：DB=AD：DB，即CD²=AD•DB，
∴（m+4）²=（m+3）（6-m），解得m₁=，m₂=-3（舍去），
∴BD=6=，CD=×+4=，
∴．
考点：一次函数图象与几何变换，勾股定理，相似三角形的判定和性质
点评：相似三角形的判定和性质是初中数学的重点，贯穿于整个初中数学的学习，是中考中比较常见的知识点，一般难度不大，需熟练掌握.