题目内容
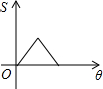
如图，两个边长相等的正方形ABCD和EFGH，正方形EFGH的顶点E固定在正方形ABCD的对称中心位置，正方形EFGH绕点E顺时针方向旋转，设它们重叠部分的面积为S，旋转的角度为θ，S与θ的函数关系的大致图象是
- A.
- B.
- C.
- D.
B
分析：过点E作EM⊥BC于点M，EN⊥AB于点N，则可证明△ENK≌△EML，从而得出重叠部分的面积不变，继而可得出函数关系图象．
解答：
解：如右图，过点E作EM⊥BC于点M，EN⊥AB于点N，
∵点E是正方形的对称中心，
∴EN=EM，
由旋转的性质可得∠NEK=∠MEL，
在Rt△ENK和Rt△EML中，
，
故可得△ENK≌△EML，即阴影部分的面积始终等于正方形面积的
．
故选B．
点评：此题考查了动点问题的函数图象，证明△ENK≌△EML，得出阴影部分的面积始终等于正方形面积的是解答本题的关键．
分析：过点E作EM⊥BC于点M，EN⊥AB于点N，则可证明△ENK≌△EML，从而得出重叠部分的面积不变，继而可得出函数关系图象．
解答：
解：如右图，过点E作EM⊥BC于点M，EN⊥AB于点N，∵点E是正方形的对称中心，
∴EN=EM，
由旋转的性质可得∠NEK=∠MEL，
在Rt△ENK和Rt△EML中，
，故可得△ENK≌△EML，即阴影部分的面积始终等于正方形面积的
．故选B．
点评：此题考查了动点问题的函数图象，证明△ENK≌△EML，得出阴影部分的面积始终等于正方形面积的
是解答本题的关键． 
练习册系列答案
高效智能课时作业系列答案
捷径训练检测卷系列答案
小夫子全能检测系列答案
相关题目
的全等的等边
与
拼成一个四边形
，把一个含
角的直角三角尺与此四边形重合，使三角尺的
重合，两边分别与
、
重合. 将三角尺绕点
）. 
、
相交于点
、
时，如图（1），①求证：1).∠BAE=∠CAF,2).
；②重叠部分（四边形
）的面积为 ．
还相等吗？说明理由；
的取值范围是 ．