Question

某课外活动小组对课本上的一道习题学习后，进行了拓展应用：
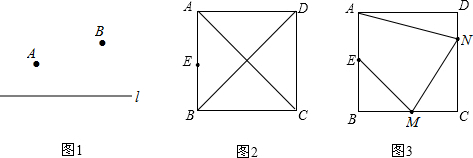
（1）如图1，是在直线l上找一点P，使得PA+PB最短（画图即可）。
（2）如图2，应用：已知正方形ABCD中，E为AB的中点，在线段BD上找一点P，使得PA+PE的值最小，并说明理由。
（3）探索：E为正方形ABCD的AB边的中点，如图3，M为BC上一点，N为CD上一点，连接EM，MN，NA，请你应用（1）的原理在图2中找出点M，N，使得EM+MN+NA的值最小，画图即可。

Answer 1

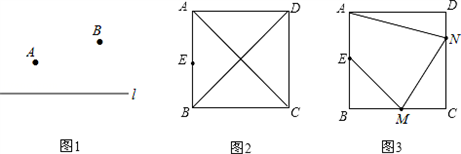
解：（1）如图所示：
（2）作E点关于BD的对称点E'，连接AE'，与BD的交点即为P点。
因为AP+PE=AP+PE'=AE'，此时A，P，E'三点共线，
所以此时此时PA+PE=AE'最小；
（3）作F 和E关于BC对称
再作G 和F关于CD对称，连接AG，
当N为AG和CD交点时最小此时M为NF和BC的交点，
理由：作了对称后有EM=FM，所以EM+MN=FM+MN≧FN，
当且仅当F，M，N，3点共线时取等号，此时最小，同理可知道EM+MN+NA最小值。