题目内容
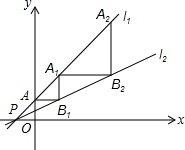 如图,直线l1:y=x+l分别交x、y轴于P、A两点,直线l2:y=
如图,直线l1:y=x+l分别交x、y轴于P、A两点,直线l2:y= x+
x+ 经过点P,过A作平行与x轴的直线交l2于点B1,再过B1作平行与y轴的直线交l1于点A1,…,依此规律作下去,则点B4的坐标为
经过点P,过A作平行与x轴的直线交l2于点B1,再过B1作平行与y轴的直线交l1于点A1,…,依此规律作下去,则点B4的坐标为
- A.(15,16)
- B.(16,8)
- C.(15,8)
- D.(31,16)
C
分析:由直线l1的解析式,求出A点的坐标,从而求出B1点的坐标,依此类推即可求得点B4的坐标.
解答: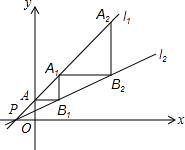 解:∵直线l1:y=x+l交y轴于A点,
解:∵直线l1:y=x+l交y轴于A点,
∴当x=0时,y=1,即A点坐标为(0,1),
∵AB1∥x轴,
∴B1点的纵坐标为1,设B1(x1,1),
∴ x1+
x1+ =1,解得x1=1;
=1,解得x1=1;
∴B1点的坐标为(1,1),即(21-1,20);
∵A1B1∥y轴,
∴A1点的横坐标为1,设A1(1,y1),
∴y1=1+1=2,
∴A1点的坐标为(1,2);
同理,可得B2(3,2),即(22-1,21);
A2(3,4);
B3(7,4),即(23-1,22);
A3(7,8);
B4(15,8),即(24-1,23).
故选C.
点评:本题考查了一次函数的综合题型,其中涉及到一次函数的性质,平行于坐标轴的直线上任意两点的坐标特点,难度适中.
分析:由直线l1的解析式,求出A点的坐标,从而求出B1点的坐标,依此类推即可求得点B4的坐标.
解答:
 解:∵直线l1:y=x+l交y轴于A点,
解:∵直线l1:y=x+l交y轴于A点,∴当x=0时,y=1,即A点坐标为(0,1),
∵AB1∥x轴,
∴B1点的纵坐标为1,设B1(x1,1),
∴
 x1+
x1+ =1,解得x1=1;
=1,解得x1=1;∴B1点的坐标为(1,1),即(21-1,20);
∵A1B1∥y轴,
∴A1点的横坐标为1,设A1(1,y1),
∴y1=1+1=2,
∴A1点的坐标为(1,2);
同理,可得B2(3,2),即(22-1,21);
A2(3,4);
B3(7,4),即(23-1,22);
A3(7,8);
B4(15,8),即(24-1,23).
故选C.
点评:本题考查了一次函数的综合题型,其中涉及到一次函数的性质,平行于坐标轴的直线上任意两点的坐标特点,难度适中.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 20、如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(a,3),则关于x的不等式x+1≥mx+n的解集为
20、如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(a,3),则关于x的不等式x+1≥mx+n的解集为 如图,直线l1、l2交于点A,试求点A的坐标.
如图,直线l1、l2交于点A,试求点A的坐标. 如图,直线l1:y=2x+4与l2:y=-x-5在同一平面角坐标系中相交于点P,则点P的坐标是
如图,直线l1:y=2x+4与l2:y=-x-5在同一平面角坐标系中相交于点P,则点P的坐标是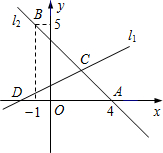 l2交于点C.
l2交于点C. 如图,直线l1,l2交于点A,直线l2与x轴交于点B,与y轴交于点D,直线l1所对应的函数关系式为y=-2x+2.
如图,直线l1,l2交于点A,直线l2与x轴交于点B,与y轴交于点D,直线l1所对应的函数关系式为y=-2x+2.