题目内容
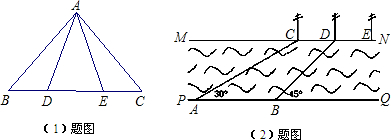
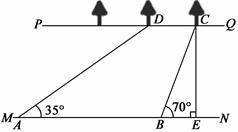
如图,河流的两岸PQ、MN互相平行,河岸PQ上有一排小树,已知相邻两树之间的距离CD=40 m,某人在河岸MN的A处测得∠DAN = 35°,然后沿河岸走了100 m到达B处,测得∠CBN=70°.求河流的宽度CE (精确到1m).
(参考数据: sin35°≈ 0.57, cos35°≈ 0.82,
tan35°≈ 0.70; sin 70°≈ 0.94, cos70°≈ 0.34,
tan70°≈ 2.75).

解:过点C作CF//DA交AB于点F.…………1分
∵ MN//PQ,CF//DA ∴四边形AFCD是平行四边形 …………………3分
∴ AF=CD=40米, ∠CFB=35°
∴ FB=AB-AF=100-40=60 ………………………………………………4分
又∵∠CBN= ∠CFB+ ∠BCF
∴ ∠BCF=70°-35°=35°= ∠CFB
∴BC=BF=60 ……………………………………………………………………6分
在Rt△BEC中, sin70°=![]()
∴CE=BC•sin70°≈60×0.94 = 56.4 ≈56(米)
答:河流的宽度CE约为56![]() 米. (本题其它方法酌情给分)…………………10分
米. (本题其它方法酌情给分)…………………10分

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目
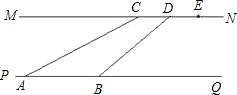 如图,河流的两岸PQ、MN互相平行,河岸MN上有一排间隔为50米的电线杆C、D、E…,某人在河岸PQ的A处测得∠CAQ=30°,然后沿河岸走了110米到达B处,测得∠DBQ=45°,求河流的宽度.
如图,河流的两岸PQ、MN互相平行,河岸MN上有一排间隔为50米的电线杆C、D、E…,某人在河岸PQ的A处测得∠CAQ=30°,然后沿河岸走了110米到达B处,测得∠DBQ=45°,求河流的宽度.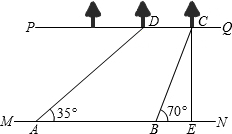 如图,河流的两岸PQ、MN互相平行,河岸PQ上有一排小树,已知相邻两树之间的距离CD=50米,某人在河岸MN的A处测得∠DAN=35°,然后沿河岸走了120米到达B处,测得∠CBN=70°.求河流的宽度CE(结果保留两个有效数字).
如图,河流的两岸PQ、MN互相平行,河岸PQ上有一排小树,已知相邻两树之间的距离CD=50米,某人在河岸MN的A处测得∠DAN=35°,然后沿河岸走了120米到达B处,测得∠CBN=70°.求河流的宽度CE(结果保留两个有效数字).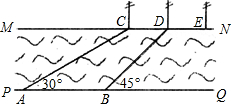 D、E、…,某人在河岸PQ的A处测得∠DBQ=45°,求河流的宽度(结果精确到0.1米).参考值:
D、E、…,某人在河岸PQ的A处测得∠DBQ=45°,求河流的宽度(结果精确到0.1米).参考值: