题目内容
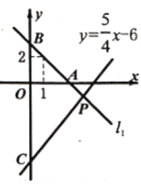
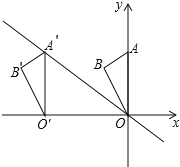
【题目】如图，在平面直角坐标系中点A的坐标为(0，6)，点B的坐标为(﹣
，5)，将△AOB沿x轴向左平移得到△A′O′B′，点A的对应点A′落在直线y＝﹣
x上，则点B的对应点B′的坐标为（ ）
A.(﹣8，6)B.(﹣
，5)C.(﹣
，5)D.(﹣8，5)
【答案】C
【解析】
根据题意确定点A′的纵坐标，根据点A′落在直线y＝﹣
x上，求出点A′的横坐标，确定△OAB沿x轴向左平移的单位长度即可得到答案．
解：由题意可知，点A移动到点A′位置时，纵坐标不变，
∴点A′的纵坐标为6，
∵点A′落在直线上y＝﹣x上，
∴﹣x＝6，解得x＝﹣8，
∴△OAB沿x轴向左平移得到△O′A′B′位置，移动了8个单位，
∴点B与其对应点B′的坐标为（﹣
，5），
故答案选：C．
练习册系列答案
全能测控期末小状元系列答案
相关题目
【题目】下表是二次函数y=ax2+bx+c的部分x,y的对应值：
x | … | －1 | － | 0 |
| 1 |
| 2 |
| 3 | … |
y | … | 2 |
| －1 | － | －2 | － | －1 |
| 2 | … |
（1）此二次函数图象的顶点坐标是 ；
（2）当抛物线y=ax2+bx+c的顶点在直线y=x+n的下方时，n的取值范围是 。
