Question

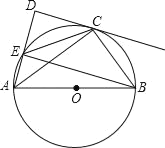
【题目】如图，AB是⊙O的弦，半径OE⊥AB，P为AB的延长线上一点，PC与⊙O相切于点C，CE与AB交于点F．

(1)求证：PC＝PF；

(2)连接OB，BC，若OB∥PC，BC＝3，tanP＝，求FB的长．

Answer 1

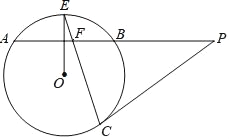
【答案】(1)证明见解析；(2)FB＝2．

【解析】

（1）连接OC，根据切线的性质以及OE⊥AB，可知∠E+∠EFA＝∠OCE+∠FCP＝90°，从而可得∠EFA＝∠FCP，继而可推得∠CFP＝∠FCP，再根据等角对等边即可证得；

（2）过点B作BG⊥PC于点G，由OB∥PC，OB＝OC，BC＝3，从而求得OB＝3，继而证得四边形OBGC是正方形，从而有OB＝CG＝BG＝3，从而有，求得PG＝4，再利用勾股定理可求得PB长，继而可求出FB长.

(1)连接OC，

∵PC是⊙O的切线，

∴∠OCP＝90°，

∵OE＝OC，

∴∠E＝∠OCE，

∵OE⊥AB，

∴∠E+∠EFA＝∠OCE+∠FCP＝90°，

∴∠EFA＝∠FCP，

∵∠EFA＝∠CFP，

∴∠CFP＝∠FCP，

∴PC＝PF；

(2)过点B作BG⊥PC于点G，

∵OB∥PC，

∴∠COB＝90°，

∵OB＝OC，BC＝3，

∴OB＝3，

∵BG⊥PC，

∴四边形OBGC是正方形，

∴OB＝CG＝BG＝3，

∵tanP＝，

∴，

∴PG＝4，

∴由勾股定理可知：PB＝5，

∵PF＝PC＝7，

∴FB＝PF﹣PB＝7﹣5＝2．