Question

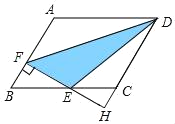
【题目】如图，在平行四边形ABCD中，AB＝3，AD＝4，∠ABC＝60°，过BC的中点E作EF⊥AB，垂足为点F，与DC的延长线相交于点H，则△DEF的面积是_____

Answer 1

【答案】2

【解析】

根据平行四边形的性质得到AB=CD=3，AD=BC=4，求出BE、BF、EF，根据全等得出CH=1，然后根据三角形的面积公式求△DEF的面积即可．

解：∵四边形ABCD是平行四边形，

∴AD=BC=4，AB∥CD，AB=CD=3，

∴∠B=∠HCE，∠H=∠BFE=90°，

∵E为BC中点，

∴BE=CE=2，

∵∠ABC=60°，EF⊥AB，

∴∠FEB=30°，

∴BF=1，

由勾股定理得：EF=，

在△BFE和△CHE中，

∵∠B=∠HCE，

∠H=∠BFE，

BE=CE，

∴△BFE≌△CHE，

∴CH=BF=1，

∴DH=1+3=4，

∴S△DEF=．

故答案为2．