题目内容
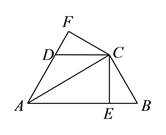
【题目】如图,边长为a的正方形ABCD和边长为b(a>b)的正方形CEFG拼在一起,B、C、E三点在同一直线上,设图中阴影部分的面积为S.



图① 图② 图③
(1)如图①,S的值与a的大小有关吗?说明理由;
(2)如图②,若a+b=10,ab=21,求S的值;
(3)如图③,若a-b=2,![]() =7,求
=7,求![]() 的值.
的值.
【答案】(1)S的值与a无关,理由见解析;(2)18.5;(3)10
【解析】分析:(1)、利用两个正方形的面积减去空白部分的面积列式即可;(2)、把a+b=10,ab=21,整体代入S1的代数式求得数值即可;(3)、首先将S进行平方,然后根据完全平方公式得出各式的值代入即可得出答案.
详解:(1)S的值与a无关,理由如下:由题意知:
S= a2+b2-![]() (a+b)a-
(a+b)a-![]() (a-b)a-
(a-b)a-![]() b2=
b2=![]() b2,∴S的值与a无关.
b2,∴S的值与a无关.
(2)∵a+b=10,ab=21,
∴S=![]() a2+b2-
a2+b2-![]() (a+b)b=
(a+b)b=![]() a2+
a2+![]() b2-
b2-![]() ab=
ab=![]() (a+b)2-
(a+b)2-![]() ab=
ab=![]() ×102-
×102-![]() ×21=50-31.5=18.5.
×21=50-31.5=18.5.
(3)∵S=![]() (a-b)a+
(a-b)a+![]() (a-b)b=
(a-b)b=![]() (a-b)(a+b),
(a-b)(a+b),
∴![]() =
=![]() (a-b)2(a+b)2.
(a-b)2(a+b)2.
∵a-b=2,∴(a-b)2=![]() ,∵
,∵![]() =7,∴
=7,∴![]() ,
,
∴![]() =
=![]() ,∴
,∴![]() =
=![]() ×4×10=10.
×4×10=10.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目