题目内容
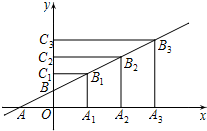 (2013•朝阳区二模)如图,在平面直角坐标系xOy中,直线AB与x、y轴分别交于点A、B,且A(-2,0),B(0,1),在直线AB上截取BB1=AB,过点B1分别作x、y轴的垂线,垂足分别为点A1、C1,得到矩形OA1B1C1;在直线AB上截取B1B2=BB1,过点B2分别作x、y轴的垂线,垂足分别为点A2、C2,得到矩形OA2B2C2;在直线AB上截取B2B3=B1B2,过点B3分别作x、y轴的垂线,垂足分别为点A3、C3,得到矩形OA3B3C3;…则第3个矩形OA3B3C3的面积是
(2013•朝阳区二模)如图,在平面直角坐标系xOy中,直线AB与x、y轴分别交于点A、B,且A(-2,0),B(0,1),在直线AB上截取BB1=AB,过点B1分别作x、y轴的垂线,垂足分别为点A1、C1,得到矩形OA1B1C1;在直线AB上截取B1B2=BB1,过点B2分别作x、y轴的垂线,垂足分别为点A2、C2,得到矩形OA2B2C2;在直线AB上截取B2B3=B1B2,过点B3分别作x、y轴的垂线,垂足分别为点A3、C3,得到矩形OA3B3C3;…则第3个矩形OA3B3C3的面积是24
24
;第n个矩形OAnBnCn的面积是2n2+2n
2n2+2n
(用含n的式子表示,n是正整数).分析:设直线AB的解析式为y=kx+b(k≠0),再把点A(-2,0),B(0,1)代入即可求出kb的值,故可得出一次函数的解析式,根据两点间的距离公式求出AB的长,设出B1,B2,B3的坐标,根据BB1=AB,B1B2=BB1,B2B3=B1B2即可得出B1,B2,B3的坐标,进而得出矩形的面积,找出规律即可得出结论.
解答:解:设直线AB的解析式为y=kx+b(k≠0),
∵点A(-2,0),B(0,1)在直线AB上,
∴
,解得
,
∴直线AB的解析式为y=
x+b,
∴AB=
=
,
设B1(x1,
x1+b),B2(x2,
x2+b),B3(x3,
x3+b)的坐标,
∵BB1=AB,B1B2=BB1,B2B3=B1B2,
∴(x1-0)2+(
x1+1-1)2=(
)2,解得x=2或x=-2(舍去),
∴B1(2,2),
同理可得B2(4,3),B3(6,4),
∴S矩形OA1B1C1=2×2=2×(1+1)=4;
S矩形OA2B2C2=4×3=2×2×(2+1)=12;
S矩形OA3B3C3=6×4=2×3×(3+1)=14,
∴第n各矩形的面积=2n(n+1)=2n2+2n.
故答案为:24;2n2+2n.
∵点A(-2,0),B(0,1)在直线AB上,
∴
|
|
∴直线AB的解析式为y=
| 1 |
| 2 |
∴AB=
| (-2-0)2+(0-1)2 |
| 5 |
设B1(x1,
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵BB1=AB,B1B2=BB1,B2B3=B1B2,
∴(x1-0)2+(
| 1 |
| 2 |
| 5 |
∴B1(2,2),
同理可得B2(4,3),B3(6,4),
∴S矩形OA1B1C1=2×2=2×(1+1)=4;
S矩形OA2B2C2=4×3=2×2×(2+1)=12;
S矩形OA3B3C3=6×4=2×3×(3+1)=14,
∴第n各矩形的面积=2n(n+1)=2n2+2n.
故答案为:24;2n2+2n.
点评:本题考查的是一次函数综合题,涉及到用待定系数法求一次函数的解析式、矩形的面积、一次函数图象上点的坐标特点等知识,难度适中.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目