Question

【题目】如图，点C在线段AB上，点M、N分别是AC、BC的中点.

（1）若AC ＝9cm，CB ＝ 6 cm，求线段MN的长；
（2）若C为线段AB上任一点，满足AC＋CB ＝ cm，其它条件不变，你能猜想MN的长度吗？并说明理由.你能用一句简洁的话描述你发现的结论吗？
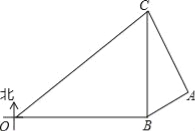
（3）若C在线段AB的延长线上，且满足AC BC ＝ b cm，M、N分别为AC、BC的中点，你能猜想MN的长度吗？请画出图形，写出你的结论，并说明理由.

Answer 1

【答案】
（1）解: ∵AC=9cm，点M是AC的中点，∴CM= AC=4.5cm，∵BC=6cm，点N是BC的中点，∴CN= BC=3cm，∴MN=CM+CN=7.5cm，∴线段MN的长度为7.5cm
（2）解: MN= a ， 当C为线段AB上一点，且M ， N分别是AC ， BC的中点，则存在MN= a
（3）解: 当点C在线段AB的延长线时，如图： 则AC＞BC ， ∵M是AC的中点，∴CM= AC ， ∵点N是BC的中点，∴CN= BC ， ∴MN=CM-CN= （AC-BC）= b
【解析】（1）根据中点的定义得出CM= AC ， CN= BC ，故MN=MC+NC=(AC+BC)，代入数据计算即可；
（2）由（1）得MN=MC+NC=×(AC+BC)，而AC+BC=acm，可得出答案；
（3）作出图后结合已知条件可知MC=×AC，NC=BC，又因为MN=MC-NC=（AC-BC）且AC-BC=bcm，即可得出答案.