题目内容
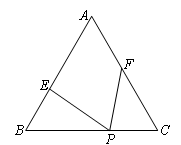
已知,等边△ABC边长为6,P为BC边上一点,且BP=4,点E、F分别在边AB、AC上,且∠EPF=60°,设BE=x,CF=y.
(1)求y与x的函数关系式,并写出x的取值范围;
(2)①若四边形AEPF的面积为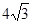 时,求x的值.
时,求x的值.
②四边形AEPF的面积是否存在最大值?若存在,请求出面积的最大值及此时x的值;若不存在,请说明理由.
(1)求y与x的函数关系式,并写出x的取值范围;
(2)①若四边形AEPF的面积为
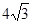 时,求x的值.
时,求x的值.②四边形AEPF的面积是否存在最大值?若存在,请求出面积的最大值及此时x的值;若不存在,请说明理由.

(1) 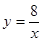 , x的取值范围是
, x的取值范围是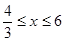 ;(2) ①4,②存在,x=2,
;(2) ①4,②存在,x=2,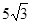 .
.
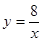 , x的取值范围是
, x的取值范围是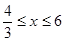 ;(2) ①4,②存在,x=2,
;(2) ①4,②存在,x=2,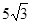 .
.试题分析:(1)求出△BEP∽△CPF,得出比例式,代入求出即可;
(2)①过A作AD⊥BC于D,过E作EN⊥BC于N,过F作FM⊥BC于M,求出AD=3
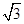 ,EN=
,EN=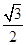 x,CF=y=
x,CF=y=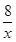 ,FM=
,FM=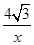 ,根据S四边形AEPF=S△ABC-S△BEP-S△CFP得出方程,求出x即可;
,根据S四边形AEPF=S△ABC-S△BEP-S△CFP得出方程,求出x即可;②四边形AEPF的面积存在最大值,把9
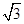 -
-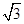 x-
x-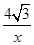 化成-
化成-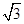 (
(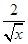 -
-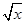 )2+5
)2+5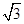 ,即可得出答案.
,即可得出答案.试题解析:(1)∵∠EPF=60°
∴∠BPE+∠CPF=120°
∵∠B=60°∴∠BPE+∠BEP=120°
∴∠BEP=∠CPF又∵∠B=∠C=60°
∴△BEP∽△CPF
∴
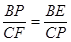
∴
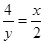
∴
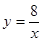 , x的取值范围是
, x的取值范围是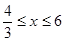 .
.(2)①过A作AD⊥BC于D,
过E作EN⊥BC于N,过F作FM⊥BC于M
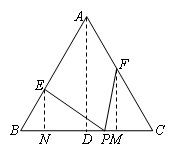
∵∠B=60°,AB=6,BE=x
∴AD=sin60°×6=
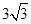 , EN=sin60°×x=
, EN=sin60°×x=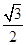 x
x ∵∠C=60°,CF=
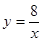 ∴FM=sin60°×
∴FM=sin60°×
∴
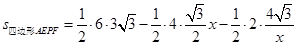
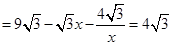 .
.∴x2-5x+4=0
∴x1=1(舍去),x2=4
②
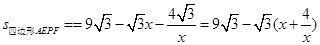
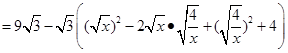
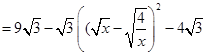
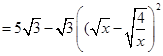
∴当
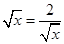 ,即x=2时,四边形AEPF的面积存在最大值,最大值是
,即x=2时,四边形AEPF的面积存在最大值,最大值是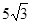 .
.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
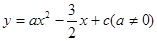 的图象与
的图象与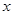 轴交于
轴交于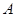 、
、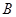 两点,与
两点,与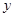 轴交于
轴交于 点,已知点
点,已知点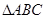 的外接圆的圆心位置,并求出圆心坐标;
的外接圆的圆心位置,并求出圆心坐标;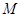 是线段
是线段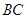 下方的抛物线上的一个动点,求
下方的抛物线上的一个动点,求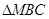 面积的最大值以及此时点
面积的最大值以及此时点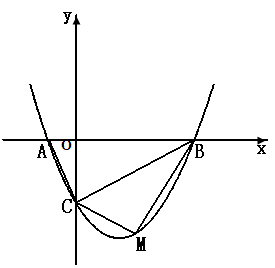
 =7.14,
=7.14, =7.21,
=7.21, =7.28,
=7.28,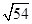 =7.35)
=7.35)
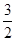 ),点M是抛物线C2:y=mx2-2mx-3m(m<0)的顶点.
),点M是抛物线C2:y=mx2-2mx-3m(m<0)的顶点.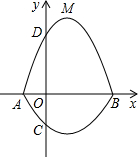
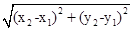 .
.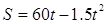 ,则飞机着陆后滑行 米才能停下来。
,则飞机着陆后滑行 米才能停下来。 的最小值”提出各自的想法.甲说:“可以利用已经学过的完全平方公式,把它配方成
的最小值”提出各自的想法.甲说:“可以利用已经学过的完全平方公式,把它配方成 ,所以代数式的最小值为-2”.乙说:“我也用配方法,但我配成
,所以代数式的最小值为-2”.乙说:“我也用配方法,但我配成 ,最小值为2”.你认为( )
,最小值为2”.你认为( )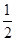 x2-7x+
x2-7x+ ,若自变量x分别取x1,x2,x3,且0<x1<x2<x3,则对应的函数值y1,y2,y3的大小关系正确的是( )
,若自变量x分别取x1,x2,x3,且0<x1<x2<x3,则对应的函数值y1,y2,y3的大小关系正确的是( )