题目内容
四边形ABCD和CEFH都是正方形,连接AE,M是AF中点,连接DM和EM.

(1)如图①,当点B、C、H在一条直线上时,线段DM与EM的位置关系是______, =______;
=______;
(2)如图②,当点B、C、F在一条直线上时,(1)中的结论还成立吗?如果成立,请证明;如果不成立,说明理由.
(1)解:延长DM交EF于点N,
∵四边形ABCD和CEFH都是正方形,
∴AD=CD,CE=EF,AD∥EF,∠CEF=90°.
∴∠AFN=∠DAF,
∵M是AF中点,
∴AM=FM.
在△ADM和△FNM中,
 ,
,
∴AD=FN.DM=MN,
∴CD=NF,
∴CE-CD=EF-NF,
即ED=EN.
∴EM⊥DN,
∵∠CEF=90°,
∴EM= DN.
DN.
∵DM= DN,
DN,
∴EM=DM.
∴DM:EM=1
故答案为:DM⊥EM,1;
(2)结论仍然成立.
证明:延长DM交BF于点N,连接ED、EN,
∵四边形ABCD、ECHF都是正方形,
∴AD=DC,EC=EF,AD∥BC,
∠DCB=∠CEF=90°,∠1=∠EFC=45°.
∴∠DAM=∠NFM.
∵M是AF的中点,∴AM=FM.
在△AMD和△FMN中,
 ,
,
∴△AMD≌△FMN(ASA).
∴AD=FN,DM=NM.
又∵AD=DC,∴DC=FN.
∵点B、C、F在一条直线上,∠1=45°,∠DCB=90°,
∴∠2=45°.
∴∠2=∠EFC.
在△EDC和△ENF中,
 ,
,
∴△EDC≌△ENF(SAS).
∴ED=EN,∠3=∠4.
∴∠3+∠CEN=∠4+∠CEN=∠CEF=90°,即∠DEN=90°.
∵ED=EN,DM=NM,
∴DM⊥EM.
∴DM=EM.
∴ .
.
分析:(1)延长DM交EF于点N,通过证明三角形全等可以得出可以得出AD=NF,DM=NM,可以求出EN=ED,根据等腰三角形的三线合一的性质可以得出EM⊥DM,DM:EM的值为1;
(2)延长DM交BF于点N,连接ED、EN,先证明△AMD≌△FMN可以得出AD=FN,DM=NM,再证明△EDC≌△ENF就可以得出ED=EN,∠3=∠4,可以得出∠DEN=90°,由等腰直角三角形的性质就可以得出结论.
点评:本题考查了正方形的性质的运用,全等三角形的判定与性质的运用,等腰直角三角形的性质的运用,解答本题的关键是作辅助线证明三角形全等.

∵四边形ABCD和CEFH都是正方形,
∴AD=CD,CE=EF,AD∥EF,∠CEF=90°.
∴∠AFN=∠DAF,
∵M是AF中点,
∴AM=FM.
在△ADM和△FNM中,
 ,
,∴AD=FN.DM=MN,
∴CD=NF,
∴CE-CD=EF-NF,
即ED=EN.
∴EM⊥DN,
∵∠CEF=90°,
∴EM=
 DN.
DN.∵DM=
 DN,
DN,∴EM=DM.
∴DM:EM=1
故答案为:DM⊥EM,1;
(2)结论仍然成立.

证明:延长DM交BF于点N,连接ED、EN,
∵四边形ABCD、ECHF都是正方形,
∴AD=DC,EC=EF,AD∥BC,
∠DCB=∠CEF=90°,∠1=∠EFC=45°.
∴∠DAM=∠NFM.
∵M是AF的中点,∴AM=FM.
在△AMD和△FMN中,
 ,
,∴△AMD≌△FMN(ASA).
∴AD=FN,DM=NM.
又∵AD=DC,∴DC=FN.
∵点B、C、F在一条直线上,∠1=45°,∠DCB=90°,
∴∠2=45°.
∴∠2=∠EFC.
在△EDC和△ENF中,
 ,
,∴△EDC≌△ENF(SAS).
∴ED=EN,∠3=∠4.
∴∠3+∠CEN=∠4+∠CEN=∠CEF=90°,即∠DEN=90°.
∵ED=EN,DM=NM,
∴DM⊥EM.
∴DM=EM.
∴
 .
.分析:(1)延长DM交EF于点N,通过证明三角形全等可以得出可以得出AD=NF,DM=NM,可以求出EN=ED,根据等腰三角形的三线合一的性质可以得出EM⊥DM,DM:EM的值为1;
(2)延长DM交BF于点N,连接ED、EN,先证明△AMD≌△FMN可以得出AD=FN,DM=NM,再证明△EDC≌△ENF就可以得出ED=EN,∠3=∠4,可以得出∠DEN=90°,由等腰直角三角形的性质就可以得出结论.
点评:本题考查了正方形的性质的运用,全等三角形的判定与性质的运用,等腰直角三角形的性质的运用,解答本题的关键是作辅助线证明三角形全等.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
 8、如图,在平行四边形ABCD和平行四边形AECF的顶点,D,E,F,B在一条直线上,则下列等式成立的是( )
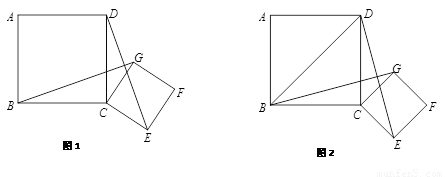
8、如图,在平行四边形ABCD和平行四边形AECF的顶点,D,E,F,B在一条直线上,则下列等式成立的是( )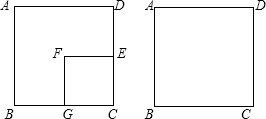 道BG=DE,如果我们把正方形CGFE绕C点顺时钟旋转90度后,解决下列问题:
道BG=DE,如果我们把正方形CGFE绕C点顺时钟旋转90度后,解决下列问题: 如图,四边形ABCD和DEFG是两个边长相等的正方形,连接CE,若∠ADG=150°,则∠DCE=
如图,四边形ABCD和DEFG是两个边长相等的正方形,连接CE,若∠ADG=150°,则∠DCE=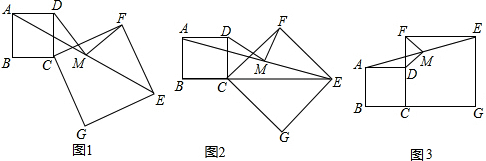
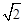 ,将正方形CEFG绕着点C旋转到某一位置时恰好使得CG//BD,BG=BD.
,将正方形CEFG绕着点C旋转到某一位置时恰好使得CG//BD,BG=BD.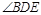 的度数;
的度数;