题目内容
已知,如图,△ABC是等边三角形,过AC边上的点D作DG∥BC,交AB于点G,在GD的延长线上取点E,使DE=DC,连接AE、BD.
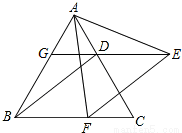
(1)求证:△AGE≌△DAB;
(2)过点E作EF∥DB,交BC于点F,连接AF,求∠AFE的度数.
(1)证明见解析;(2)60°.
【解析】
试题分析:(1)根据SAS判定△AGE和△DAB全等;
(2)证明四边形DEFB是平行四边形,△AEF是个等边三角形.
试题解析:(1)证明:∵△ABC是等边三角形,DG∥BC,
∴∠AGD=∠ABC=60°,∠ADG=∠ACB=60°,且∠BAC=60°,
∴△AGD是等边三角形,
AG=GD=AD,∠AGD=60°.
∵DE=DC,∴GE=GD+DE=AD+DC=AC=AB,
∴在△AGE与△DAB中,

∴△AGE≌△DAB(SAS);
(2)【解析】
由(1)知AE=BD,∠ABD=∠AEG.
∵EF∥DB,DG∥BC,
∴四边形BFED是平行四边形.
∴EF=BD,
∴EF=AE.
∵∠DBC=∠DEF,
∴∠ABD+∠DBC=∠AEG+∠DEF,即∠AEF=∠ABC=60°.
∴△AFE是等边三角形,∠AFE=60°.
考点:1.全等三角形的判定;2.等边三角形的性质.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
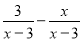
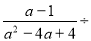
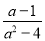
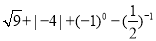

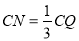 ,设运动时间为t(t>0)秒.
,设运动时间为t(t>0)秒.

 则
则  的值为( )
的值为( ) ,再选取一个恰当的
,再选取一个恰当的 值代入求值.
值代入求值. 无解,则m的值为 .
无解,则m的值为 . |=( )
|=( )