题目内容
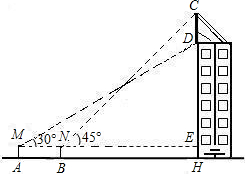
 某广电大楼顶部有一发射塔,在地面B处测得楼顶仰角为30°,测得塔顶A仰角为45°,在楼顶D处测得测得塔顶仰角为60°,若地面B处距楼底距离BC为
某广电大楼顶部有一发射塔,在地面B处测得楼顶仰角为30°,测得塔顶A仰角为45°,在楼顶D处测得测得塔顶仰角为60°,若地面B处距楼底距离BC为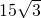 米.
米.
(1)求楼高DC.
(2)求铁塔高度(AE的长).
 解:(1)根据题意:在Rt△BDC中,有tan∠DBC=
解:(1)根据题意:在Rt△BDC中,有tan∠DBC= =
= ;
;则DC=BC×tan30°=15米.
(2)在Rt△ABF中,有AF=BF,
在Rt△ADE中,有AE=DE×tan60°,
且CF=BF-BC,BC=15
 ,DC=15米,
,DC=15米,设AE=x,则DE=
 x,
x,∴AE+EF=BC+CF,
∴x+15=15
 +
+ x,
x,解可得:AE=15
 米.
米.分析:(1)首先分析图形:根据题意构造直角三角形Rt△BDC;解即可得;
(2)题涉及到多个直角三角形,应利用其公共边构造方程关系式,进而可解即可求出答案.
点评:本题要求学生借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
 留一位小数)
留一位小数) 某广电大楼顶部有一发射塔,在地面B处测得楼顶仰角为30°,测得塔顶A仰角为45°,在楼顶D处测得测得塔顶仰角为60°,若地面B处距楼底距离BC为
某广电大楼顶部有一发射塔,在地面B处测得楼顶仰角为30°,测得塔顶A仰角为45°,在楼顶D处测得测得塔顶仰角为60°,若地面B处距楼底距离BC为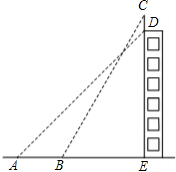 如图,某幢大楼顶部有一块3米高的广告牌CD,小明在A点测得点D的仰角是45°,走近9米在B点测得点C的仰角是60°,且A、B、E三点在一条直线上.求这幢大楼DE的高度(
如图,某幢大楼顶部有一块3米高的广告牌CD,小明在A点测得点D的仰角是45°,走近9米在B点测得点C的仰角是60°,且A、B、E三点在一条直线上.求这幢大楼DE的高度( 米.
米.