题目内容
(1)计算:
(2)计算:(-2m2n-2)2•(3m-1n3)-3
(3)已知x2-2=0,求代数式 的值.
的值.
解:(1)原式=3-1+3 -4
-4 =2-
=2- ;
;
(2)原式=4m4n-4• m3n-9=
m3n-9= m7n=-13;
m7n=-13;
(3)原式= +
+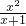 =
= +
+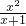 =
=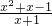 ,
,
∵x2-2=0,∴x= 或-
或- ,
,
则原式=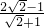 =
=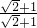 或
或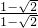 =1.
=1.
分析:(1)原式第一项利用负指数幂法则计算,第二项利用零指数幂法则计算,第三项化为最简二次根式,最后一项先计算乘方运算,再计算乘法运算,即可得到结果;
(2)原式先利用积的乘方与幂的乘方运算法则计算,再利用单项式乘单项式法则计算即可得到结果;
(3)原式通分并利用同分母分式的加法法则计算,由已知等式求出x的值,代入计算即可求出值.
点评:此题考查了分式的化简求值,负指数幂与零指数幂,分式的加减运算关键是通分,通分的关键是找最简公分母;分式的乘除运算关键是约分,约分的关键是找公因式.
 -4
-4 =2-
=2- ;
;(2)原式=4m4n-4•
 m3n-9=
m3n-9= m7n=-13;
m7n=-13;(3)原式=
 +
+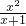 =
= +
+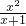 =
=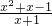 ,
,∵x2-2=0,∴x=
 或-
或- ,
,则原式=
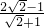 =
=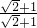 或
或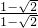 =1.
=1.分析:(1)原式第一项利用负指数幂法则计算,第二项利用零指数幂法则计算,第三项化为最简二次根式,最后一项先计算乘方运算,再计算乘法运算,即可得到结果;
(2)原式先利用积的乘方与幂的乘方运算法则计算,再利用单项式乘单项式法则计算即可得到结果;
(3)原式通分并利用同分母分式的加法法则计算,由已知等式求出x的值,代入计算即可求出值.
点评:此题考查了分式的化简求值,负指数幂与零指数幂,分式的加减运算关键是通分,通分的关键是找最简公分母;分式的乘除运算关键是约分,约分的关键是找公因式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
随机抽取某城市30天的空气质量状况统计如下:
其中,ω≤50时,空气质量为优;50<ω≤100时,空气质量为良;100<ω≤150时,空气质量为轻微污染.
(1)请分别算出这30天里空气质量为优、良、轻微污染所占的百分比;
(2)请用扇形统计图表示(1)的计算结果;
(3)估计该城市一年(以365天计)中有多少天空气质量达到良以上.
| 污染指数(ω) | 40 | 70 | 90 | 110 | 120 | 140 |
| 天数(t) | 3 | 5 | 10 | 7 | 4 | 1 |
(1)请分别算出这30天里空气质量为优、良、轻微污染所占的百分比;
(2)请用扇形统计图表示(1)的计算结果;
(3)估计该城市一年(以365天计)中有多少天空气质量达到良以上.



