题目内容
14.已知,如图,AB是⊙O的直径,C为⊙O上一点,AD垂直于经过点C的直线DE,垂足为点D,AC平分∠DAB.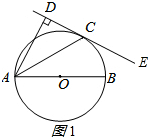
(1)求证:直线DE是⊙O的切线;
(2)连接BC,猜想:∠ECB与∠CAB的数量关系,并证明你的猜想.
分析 (1)连接OC,由等腰三角形的性质和已知条件得出∠ACO=∠DAC,证出AD∥OC,再由已知条件得出OC⊥DE,即可得出直线DE是⊙O的切线;
(2)由圆周角定理得出∠ACB=90°,得出∠CAB+∠B=90°,得出∠ECB+∠BCO=90°,由等腰三角形的性质得出∠B=∠BCO,即可得出结论.
解答 (1)证明:连接OC,如图1所示: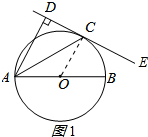
∵OA=OC,
∴∠BAC=∠ACO,
∵AC平分∠DAB,
∴∠DAC=∠BAC,
∴∠ACO=∠DAC,
∴AD∥OC,
∵AD⊥DE,
∴OC⊥DE,
∴直线DE是⊙O的切线;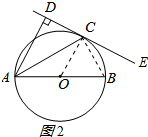
(2)解:如图2所示:∠ECB=∠CAB,理由如下:
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠CAB+∠B=90°,
∵OC⊥DE,
∴∠ECB+∠BCO=90°,
∵OC=OB,
∴∠B=∠BCO,
∴∠ECB=∠CAB.
点评 本题考查了切线的判定、等腰三角形的性质、平行线的判定、圆周角定理;熟练掌握切线的判定方法,由等腰三角形的性质得出角相等是解决问题的关键.

练习册系列答案
相关题目
9.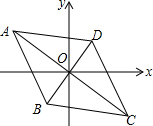 如图,菱形ABCD的对角线相交于坐标原点,点A的坐标为(a,2),点B的坐标为(-1,-$\sqrt{3}$),点C的坐标为(2$\sqrt{3}$,c),那么a,c的值分别是( )
如图,菱形ABCD的对角线相交于坐标原点,点A的坐标为(a,2),点B的坐标为(-1,-$\sqrt{3}$),点C的坐标为(2$\sqrt{3}$,c),那么a,c的值分别是( )
 如图,菱形ABCD的对角线相交于坐标原点,点A的坐标为(a,2),点B的坐标为(-1,-$\sqrt{3}$),点C的坐标为(2$\sqrt{3}$,c),那么a,c的值分别是( )
如图,菱形ABCD的对角线相交于坐标原点,点A的坐标为(a,2),点B的坐标为(-1,-$\sqrt{3}$),点C的坐标为(2$\sqrt{3}$,c),那么a,c的值分别是( )| A. | a=-1,c=-$\sqrt{3}$ | B. | a=-2$\sqrt{3}$,c=-2 | C. | a=1,c=$\sqrt{3}$ | D. | a=2$\sqrt{3}$,c=2 |
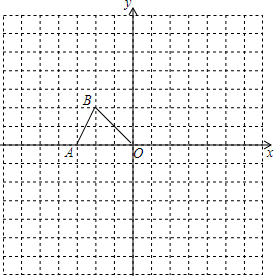 如图,在平面直角坐标系中,△AOB的位置如图所示,图中小正方形的边长均为1,请画出△AOB以点O为位似中心,放大到原来的2倍的位似图形,并写出放大后三角形三个顶点的坐标.
如图,在平面直角坐标系中,△AOB的位置如图所示,图中小正方形的边长均为1,请画出△AOB以点O为位似中心,放大到原来的2倍的位似图形,并写出放大后三角形三个顶点的坐标.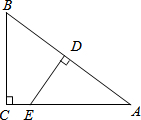 如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,边D点作AB的垂线交AC于点E,AC=8,cosA=$\frac{4}{5}$,则DE=$\frac{15}{4}$.
如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,边D点作AB的垂线交AC于点E,AC=8,cosA=$\frac{4}{5}$,则DE=$\frac{15}{4}$. 如图,在△ABC中,∠ABC=50°,∠ACB=60°,点E在BC的延长线上,∠ABC的平分线BD与∠ACE的平分线CD相交于点D,连接AD,以下结论:①∠BAC=70°;②∠DOC=90°;③∠BDC=35°;④∠DAC=55°,其中正确的是①③④.(填写序号)
如图,在△ABC中,∠ABC=50°,∠ACB=60°,点E在BC的延长线上,∠ABC的平分线BD与∠ACE的平分线CD相交于点D,连接AD,以下结论:①∠BAC=70°;②∠DOC=90°;③∠BDC=35°;④∠DAC=55°,其中正确的是①③④.(填写序号)