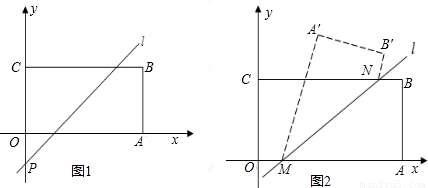
题目内容
 如图,已知直线l把平行四边形分成两部分,但l不经过四边形各顶点和各边中点,
如图,已知直线l把平行四边形分成两部分,但l不经过四边形各顶点和各边中点,(1)是否存在这样的直线把这个平行四边形的面积分成相等的两部分
存在
存在
.(2)如果存在,这样的直线l有几条,说明它的位置,如果不存在,说明理由:
经过该平行线四边形中心的直线l均满足条件(除经过顶点和各边中点的直线l)
经过该平行线四边形中心的直线l均满足条件(除经过顶点和各边中点的直线l)
.分析:平行四边形是中心对称图形,根据中心对称图形的性质,经过对称中心的任意一条直线都把它分成两个全等形,面积当然相等.
解答: 解:(1)存在这样的直线把这个平行四边形的面积分成相等的两部分.
解:(1)存在这样的直线把这个平行四边形的面积分成相等的两部分.
故答案是:存在;
(2)这样的直线l有无数条.理由如下:
如图所示,分别连接AC、BD,且相交于点O,然后作直线PO,与平行四边形相交于E、F两点,
则四边形ABFE和四边形FCDE面积相等.
故答案是:经过该平行线四边形中心的直线l均满足条件(除经过顶点和各边中点的直线l).
 解:(1)存在这样的直线把这个平行四边形的面积分成相等的两部分.
解:(1)存在这样的直线把这个平行四边形的面积分成相等的两部分.故答案是:存在;
(2)这样的直线l有无数条.理由如下:
如图所示,分别连接AC、BD,且相交于点O,然后作直线PO,与平行四边形相交于E、F两点,
则四边形ABFE和四边形FCDE面积相等.
故答案是:经过该平行线四边形中心的直线l均满足条件(除经过顶点和各边中点的直线l).
点评:本题考查了中心对称,平行四边形的性质.其中根据题意得出直线过平行四边形的中心M是解本题的关键.

练习册系列答案
相关题目
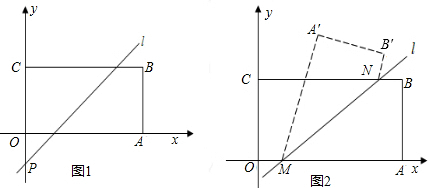
 )并把矩形OABC的面积平均分为两部分,求直线l的函数表达式;
)并把矩形OABC的面积平均分为两部分,求直线l的函数表达式;
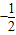 )并把矩形OABC的面积平均分为两部分,求直线l的函数表达式;
)并把矩形OABC的面积平均分为两部分,求直线l的函数表达式;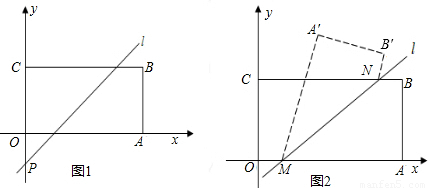
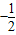 )并把矩形OABC的面积平均分为两部分,求直线l的函数表达式;
)并把矩形OABC的面积平均分为两部分,求直线l的函数表达式;