题目内容
已知等腰三角形两边长分别为5和8，则底角的余弦值为分析：先确定等腰三角形的腰长，分两种情况讨论，当边长为5和边长为8时，作底边的高，构成直角三角形，然后根据锐角三角函数的定义求解．
解答：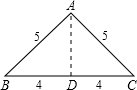
解：（1）当等腰三角形ABC的腰长为5，底边长8时，
作底边BC的高AD，则BD=CD=4，
在Rt△ADB中，
∴cos∠B=
=
；
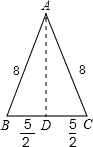
（2）当等腰三角形ABC的腰长为8，底边长5时，
作底边BC的高AD，则BD=CD=
，
在Rt△ADB中，
∴cos∠B=
=
．
故答案为
或
．
解：（1）当等腰三角形ABC的腰长为5，底边长8时，作底边BC的高AD，则BD=CD=4，
在Rt△ADB中，
∴cos∠B=
| BD |
| AB |
| 4 |
| 5 |
（2）当等腰三角形ABC的腰长为8，底边长5时，
作底边BC的高AD，则BD=CD=
| 5 |
| 2 |
在Rt△ADB中，
∴cos∠B=
| BD |
| AB |
| 5 |
| 16 |
故答案为
| 4 |
| 5 |
| 5 |
| 16 |
点评：本题考查了等腰三角形的性质、勾股定理以及锐角三角函数的定义，此题综合性较强，难度适中，易于掌握．
练习册系列答案
相关题目