题目内容
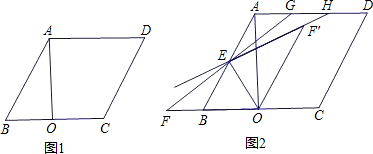
如图1,在□ABCD中,AE⊥BC于E,E恰为BC的中点,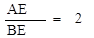 .
.
(1)求证:AD=AE;
(2)如图2,点P在BE上,作EF⊥DP于点F,连结AF. 求证: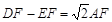 ;
;
(3)请你在图3中画图探究:当P为射线EC上任意一点(P不与点E重合)时,作EF⊥DP于点F,连结AF,线段DF、EF与AF之间有怎样的数量关系?直接写出你的结论.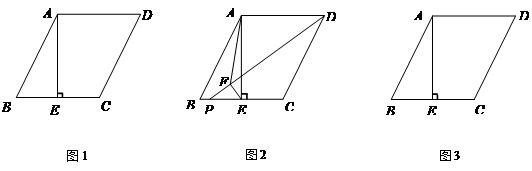
(1)在Rt△ABE中,∠AEB=90°,
∴ 
∴ .
.
∴ .
.
∴AE="BC."
∵ABCD是平行四边形,
∴AD="BC."
∴AE="AD."
(2)在DP上截取DH=EF(如图8).
∵四边形ABCD是平行四边形,AE⊥BC,
∴∠EAD=90°.
∵EF⊥PD,∠1=∠2,
∴∠ADH=∠AEF.
∵AD=AE,
∴△ADH≌△AEF.
∴∠HAD=∠FAE,AH=AF.
∴∠FAH ==90°.
在Rt△FAH中, AH=AF,
∴ .
.
∴ .
.
即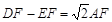 .
.
(3)按题目要求所画图形见图9,
线段DF、EF、AF之间的数量
关系为: .
.
解析

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
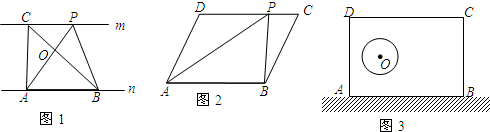



 )时,作EF⊥DP于点F,连接AF,线段DF、EF与AF之间有怎样的数量关系?直接写出你的结论.
)时,作EF⊥DP于点F,连接AF,线段DF、EF与AF之间有怎样的数量关系?直接写出你的结论.