Question

【题目】如图，⊙O是△ABC的外接圆，AB是⊙O的直径，FO⊥AB，垂足为点O，连接AF并延长交⊙O于点D，连接OD交BC于点E，∠B=30°，FO=．

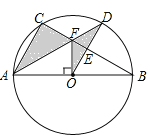
（1）求AC的长度；

（2）求图中阴影部分的面积．（计算结果保留根号）

Answer 1

【答案】（1）6；（2）．

【解析】

试题分析：（1）由∠BOF=90°，∠B=30°，得出FO=， OB=6，AB=2OB=12，由AB为⊙O的直径，得到∠ACB=90°，故AC=AB=6；

（2）先证Rt△ACF≌Rt△AOF，得出阴影部分的面积=△AOD的面积，求出三角形的面积即可．

试题解析：解：（1）∵OF⊥AB，

∴∠BOF=90°，

∵∠B=30°，FO=，

∴OB=6，AB=2OB=12，

又∵AB为⊙O的直径，

∴∠ACB=90°，

∴AC=AB=6；

（2）∵由（1）可知，AB=12，

∴AO=6，即AC=AO，

在Rt△ACF和Rt△AOF中，

∴Rt△ACF≌Rt△AOF，

∴∠FAO=∠FAC=30°，

∴∠DOB=60°，

过点D作DG⊥AB于点G，

∵OD=6，∴DG=，

∴，即．