题目内容
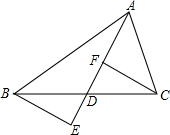
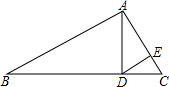 如图,已知:AD是Rt△ABC斜边BC上的高线,DE是Rt△ADC斜边AC上的高线,如果DC:AD=1:2,S△ADE=a,那么S△ABC等于
如图,已知:AD是Rt△ABC斜边BC上的高线,DE是Rt△ADC斜边AC上的高线,如果DC:AD=1:2,S△ADE=a,那么S△ABC等于
- A.4a
- B.9a
- C.16a
- D.
 a
a
D
分析:先证△ABD∽△CAD,得到 ,再证△ADE∽△BAC,可得S△ABC:S△ADE=
,再证△ADE∽△BAC,可得S△ABC:S△ADE= =
= ,即S△ABC=
,即S△ABC= .
.
解答:设DC=x,AD=2x
∵∠ABD+∠ACD=90°,∠ACD+∠CAD=90°
∴∠ABD=∠CAD
又∵∠ADB=∠CDA
∴△ABD∽△CAD
∴
∴BD=4x
∴BC=5x
同理可证出△ADE∽△BAC
∴S△ABC:S△ADE= =
=
∴S△ABC= .
.
故选D.
点评:此题考查了相似三角形的判定和性质,以及相似三角形的面积比等于相似比的平方.
分析:先证△ABD∽△CAD,得到
 ,再证△ADE∽△BAC,可得S△ABC:S△ADE=
,再证△ADE∽△BAC,可得S△ABC:S△ADE= =
= ,即S△ABC=
,即S△ABC= .
.解答:设DC=x,AD=2x
∵∠ABD+∠ACD=90°,∠ACD+∠CAD=90°
∴∠ABD=∠CAD
又∵∠ADB=∠CDA
∴△ABD∽△CAD
∴

∴BD=4x
∴BC=5x
同理可证出△ADE∽△BAC
∴S△ABC:S△ADE=
 =
=
∴S△ABC=
 .
.故选D.
点评:此题考查了相似三角形的判定和性质,以及相似三角形的面积比等于相似比的平方.

练习册系列答案
相关题目

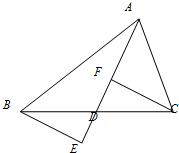 23、如图,已知:AD是BC上的中线,E点在AD延长线上,且DF=DE.
23、如图,已知:AD是BC上的中线,E点在AD延长线上,且DF=DE.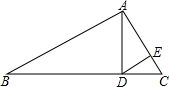 如图,已知:AD是Rt△ABC斜边BC上的高线,DE是Rt△ADC斜边AC上的高线,如果DC:AD=1:2,S△CDE=a,那么S△ABC等于( )
如图,已知:AD是Rt△ABC斜边BC上的高线,DE是Rt△ADC斜边AC上的高线,如果DC:AD=1:2,S△CDE=a,那么S△ABC等于( )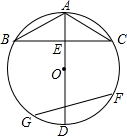 如图,已知:AD是⊙O的直径,AB、AC是弦,且AB=AC.
如图,已知:AD是⊙O的直径,AB、AC是弦,且AB=AC.
 如图,已知:AD是BC上的中线,BE⊥AD于点E,且DF=DE.求证:CF⊥AD.
如图,已知:AD是BC上的中线,BE⊥AD于点E,且DF=DE.求证:CF⊥AD.