题目内容
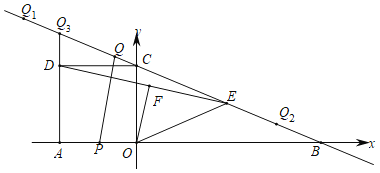
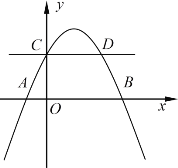
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]()
![]() ,
,![]() 两点,交
两点,交![]() 轴于点C,与过点C且平行于x轴的直线交于另一点
轴于点C,与过点C且平行于x轴的直线交于另一点![]() ,点P是抛物线上一动点.
,点P是抛物线上一动点.
(1)求抛物线解析式及点D的坐标;
(2)点![]() 在
在![]() 轴上,若以
轴上,若以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形,求此时点
为顶点的四边形是平行四边形,求此时点![]() 的坐标;
的坐标;
(3)过点![]() 作直线CD的垂线,垂足为
作直线CD的垂线,垂足为![]() ,若将
,若将![]() 沿
沿![]() 翻折,点
翻折,点![]() 的对应点为
的对应点为![]() .是否存在点
.是否存在点![]() ,使
,使![]() 恰好落在
恰好落在![]() 轴上?若存在,求出此时点P的坐标;若不存在,说明理由.
轴上?若存在,求出此时点P的坐标;若不存在,说明理由.
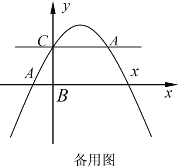
【答案】(1)![]() ;点
;点![]() 坐标为
坐标为![]() ; (2)P1(0,2); P2(
; (2)P1(0,2); P2(![]() ,-2);P3(
,-2);P3(![]() ,-2) ; (3)满足条件的点
,-2) ; (3)满足条件的点![]() 有两个,其坐标分别为:(
有两个,其坐标分别为:(![]() ,
, ![]() ),(
),(![]() ,
,![]() ).
).
【解析】
1)用待定系数法可得出抛物线的解析式,令y=2可得出点D的坐标
(2)分两种情况进行讨论,①当AE为一边时,AE∥PD,②当AE为对角线时,根据平行四边形对顶点到另一条对角线距离相等,求解点P坐标
(3)结合图形可判断出点P在直线CD下方,设点P的坐标为(![]() ,
,![]() ),分情况讨论,①当P点在y轴右侧时,②当P点在y轴左侧时,运用解直角三角形及相似三角形的性质进行求解即可
),分情况讨论,①当P点在y轴右侧时,②当P点在y轴左侧时,运用解直角三角形及相似三角形的性质进行求解即可
(1)∵抛物线![]() 经过
经过![]()
![]() ,
,![]()
![]() 两点,
两点,
∴![]() ,解得:
,解得:![]() ,
,![]() ,
,
∴抛物线解析式为:![]() ;
;
当![]() 时,
时,![]() ,解得:
,解得:![]() ,
,![]() (舍),即:点
(舍),即:点![]() 坐标为
坐标为![]() .
.
(2)∵![]() ,
,![]() 两点都在
两点都在![]() 轴上,∴
轴上,∴![]() 有两种可能:
有两种可能:
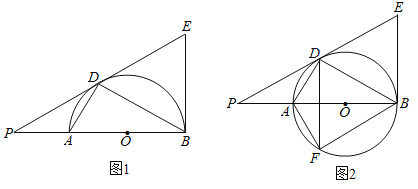
①当![]() 为一边时,
为一边时,![]() ∥
∥![]() ,此时点
,此时点![]() 与点
与点![]() 重合(如图1),∴
重合(如图1),∴![]() ,
,
②当![]() 为对角线时,
为对角线时,![]() 点、
点、![]() 点到直线
点到直线![]() (即
(即![]() 轴)的距离相等,
轴)的距离相等,
∴![]() 点的纵坐标为
点的纵坐标为![]() (如图2),
(如图2),
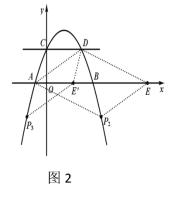
把![]() 代入抛物线的解析式,得:
代入抛物线的解析式,得:![]() ,
,
解得:![]() ,
,![]() ,
,
∴![]() 点的坐标为
点的坐标为![]() ,
,![]() ,
,
综上所述:![]() ;
; ![]()
![]() ;
;![]()
![]() .
.
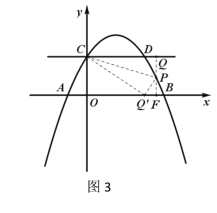
(3)存在满足条件的点![]() ,显然点
,显然点![]() 在直线
在直线![]() 下方,设直线
下方,设直线![]() 交
交![]() 轴于
轴于![]() ,
,
点![]() 的坐标为(
的坐标为(![]() ,
,![]() ),
),
①当![]() 点在
点在![]() 轴右侧时(如图3),
轴右侧时(如图3),
![]() ,
,
![]()
![]()
![]() ,
,
又∵![]()
![]() ,
,
![]() ∴
∴![]() ,
,
又![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,![]()
![]() ,∴
,∴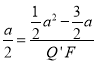 ,∴
,∴![]() ,
,
∴![]()
![]() ,
,![]() =
=![]() =
=![]() ,
,
即![]() ,∴点
,∴点![]() 的坐标为(
的坐标为(![]() ,
,![]() ),
),
②当![]() 点在
点在![]() 轴左侧时(如图4),
轴左侧时(如图4),
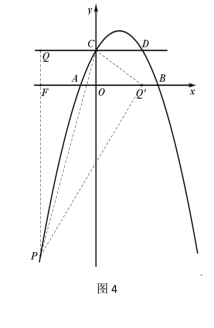
此时![]() ,
,![]() ,
,![]() =
=![]() =
=![]() ,
,
![]() =
=![]() -(
-(![]() )=
)=![]() ,
,
又∵![]() ,
,![]() ,
,
∴![]() ,又
,又![]()
∴![]() ,∴
,∴![]() ,
,
∵![]() ,
,![]() ,
,![]()
![]() ,
,
∴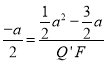 ,∴
,∴![]() ,
,
∴![]() ,
,
![]() =
=![]() =
=![]() ,
,
此时![]() ,点
,点![]() 的坐标为(
的坐标为(![]() ,
,![]() ).
).
综上所述,满足条件的点![]() 有两个,其坐标分别为:(
有两个,其坐标分别为:(![]() ,
,![]() ),(
),(![]() ,
,![]() ).
).

【题目】中华文明,源远流长;中华汉字,寓意深广.为传承中华优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛.为了解本次大赛的成绩,校团委随机抽取了其中200名学生的成绩作为样本进行统计,制成如下不完整的统计图表:
频数频率分布表
成绩x(分) | 频数(人) | 频率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | 40 | n |
80≤x<90 | m | 0.35 |
90≤x≤100 | 50 | 0.25 |
根据所给信息,解答下列问题:
(1)m= ,n= ;
(2)补全频数分布直方图;
(3)这200名学生成绩的中位数会落在 分数段;
(4)若成绩在90分以上(包括90分)为“优”等,请你估计该校参加本次比赛的3000名学生中成绩是“优”等的约有多少人?