题目内容
【题目】在△ABC中,AB=AC=5,BC=6,D,E分别是边AB,AC上的两个动点(D不与A,B重合),且保持DE∥BC，以DE为边，在点A的异侧作正方形DEFG.
(1)当FG与BC重合时，求正方形DEFG的边长；
(2)设AD=x，△ABC与正方形DEFG重叠部分的面积为y，试求y关于x的函数关系式，并写出x的取值范围；
(3)当△BDG是等腰三角形时，请直接写出AD的长.
【答案】(1) 
；(2) 
或 
； (3) 
或
或
；
【解析】
（1）首先设BC边上的高AM交DE天点P．由在△ABC中，AB=AC=5，BC=6，即可求得BM与AM的值，又由DE∥BC，可得△ADE∽△ABC，根据相似三角形高的比等于相似比，即可得方程：
，解此方程即可求得答案；
（2）首先根据三角函数的定义求得正方形DEFG的边长为
，然后分别从当FG在△ABC的内部时与当FG在△ABC的外部时去分析求解即可求得答案；
（3）分别从GB=GD，DB=DG，BD=BG去分析求解即可求得答案．
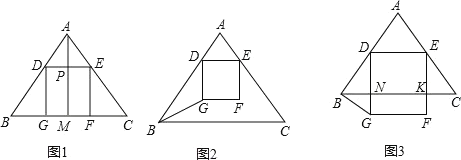
(1)如图1，设BC边上的高AM交DE于点P.
∵AB=AC=5，BC=6，且AM⊥BC，
∴BM=
BC=3,∴AM=
,
∵DE∥BC，
∴△ADE∽△ABC,
∴
,
设正方形DEFG的边长为a，
则,
∴a=，
∴当FG与BC重合时,正方形DEFG的边长为.
(2)在Rt△ADP中,DP=
AD=x，
∴正方形DEFG的边长为
x.
①如图2,当FG在△ABC的内部时,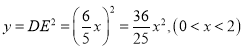 
;
②如图3，当FG与BC重合或在△ABC的外部时，设DG与BC交于点N.
在Rt△DBN中, 
.
∴
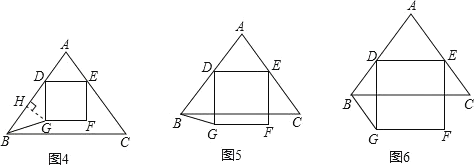
(3)如图4，当GB=GD时，过点G作GH⊥AB于H，
则DH=BH，
∵AD=x,DG=x，
∴DH=
DG=
x,
∵AD+DB=5，
∴x+x+x=5，
解得：x=，
则AD=;
如图5，当DB=DG时，
则AB=AD+DB=AD+DG，
即x+x=5，
解得x=，
即AD=;
如图6，当BD=BG时，
BD=
=
DG=x=
x，
∵AD+BD=AB=5，
∴x+x=5，
解得：x=，
∴AD=.
∴当△BDG是等腰三角形时,AD=或或
.
