Question

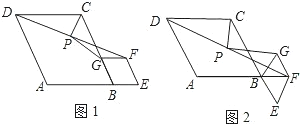
23、如图1，在菱形ABCD中，AE⊥BC，AF⊥CD，垂足为E、F．
（1）求证：△ABE≌△ADF；
（2）若∠BAE=∠EAF，求证：AE=BE；
（3）若对角线BD与AE、AF交于点M、N，且BM=MN（如图2）．求证：∠EAF=2∠BAE．

Answer 1

分析：（1）根据菱形的性质，由AAS证明△ABE≌△ADF；
（2）欲证AE=BE，可以通过证明∠B=45°=∠BAE，根据等腰直角三角形的性质得出；
（3）由于∠BAN=90°，通过证明△AMN是等边三角形，得出∠MAN=60°，则有∠MAB=30°，从而证明∠EAF=2∠BAE．

解答：解：（1）∵菱形ABCD，
∴AB=AD，∠ABE=∠ADF，（2分）
又∵AE⊥BC，AF⊥CD，
∴∠AEB=∠AFD，（1分）
∴△ABE≌△ADF．（1分）

（2）∵菱形ABCD，
∴AB∥CD，
又∵AF⊥CD，
∴AF⊥AB，
∴∠BAF=90°，又∠BAE=∠EAF，
∴∠BAE=45°，∠AEB=90°，（2分）
∴∠B=45°=∠BAE，（1分）
∴AE=BE．（1分）

（3）∵△ABE≌△ADF，
∴∠BAE=∠DAF，AB=AD，
∴∠ABM=∠ADN，
∴△ABM≌△ADN．
∴AM=AN，（1分）
又∵∠BAN=90°，BM=MN，
∴AM=MN=AN，
∴∠MAN=60°，（1分）
∴∠MAB=30°，（1分）
∴∠EAF=2∠BAE．（1分）

点评：本题是推理证明题，主要考查菱形的边的性质，同时综合利用全等三角形的判定方法及等腰三角形和等边三角形的性质．