题目内容
(2013•陕西)已知两点A(-5,y1),B(3,y2)均在抛物线y=ax2+bx+c(a≠0)上,点C(x0,y0)是该抛物线的顶点.若y1>y2≥y0,则x0的取值范围是( )
分析:先判断出抛物线开口方向上,进而求出对称轴即可求解.
解答:解:∵点C(x0,y0)是抛物线的顶点,y1>y2≥y0,
∴抛物线有最小值,函数图象开口向上,
∴a>0;∴25a-5b+c>9a+3b+c,
∴
<1,∴-
>-1,
∴x0>-1
∴x0的取值范围是x0>-1.
故选B.
∴抛物线有最小值,函数图象开口向上,
∴a>0;∴25a-5b+c>9a+3b+c,
∴
| b |
| 2a |
| b |
| 2a |
∴x0>-1
∴x0的取值范围是x0>-1.
故选B.
点评:本题考查了二次函数图象上点坐标特征,主要利用了二次函数的增减性与对称性,根据顶点的纵坐标最小确定出抛物线开口方向上是解题的关键.

练习册系列答案
相关题目
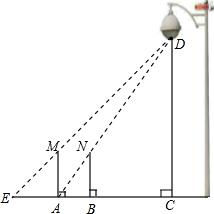 (2013•陕西)一天晚上,黎明和张龙利用灯光下的影子长来测量一路灯D的高度.如图,当李明走到点A处时,张龙测得李明直立时身高AM与影子长AE正好相等;接着李明沿AC方向继续向前走,走到点B处时,李明直立时身高BN的影子恰好是线段AB,并测得AB=1.25m,已知李明直立时的身高为1.75m,求路灯的高CD的长.(结果精确到0.1m).
(2013•陕西)一天晚上,黎明和张龙利用灯光下的影子长来测量一路灯D的高度.如图,当李明走到点A处时,张龙测得李明直立时身高AM与影子长AE正好相等;接着李明沿AC方向继续向前走,走到点B处时,李明直立时身高BN的影子恰好是线段AB,并测得AB=1.25m,已知李明直立时的身高为1.75m,求路灯的高CD的长.(结果精确到0.1m).