题目内容
【题目】如图，在矩形ABCD中，P为AD上一点，连接BP，CP，过C作CE⊥BP于点E，连接ED交PC于点F．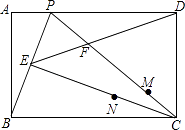
（1）求证：△ABP∽△ECB；
（2）若点E恰好为BP的中点，且AB=3，AP=k（0＜k＜3）．
①求 
的值（用含k的代数式表示）；
②若M、N分别为PC，EC上的任意两点，连接NF，NM，当k= 
时，求NF+NM的最小值．
【答案】
（1）
证明：在矩形ABCD中，
∵∠A=∠ABC=90°，
∵CE⊥BP，
∴∠CEB=90°，
∴∠A=∠CEB，
∴∠APB+∠ABP=∠ABP+∠PBC=90°，
∴∠APB=∠PBC，
∴△ABP∽△ECB
（2）
解：①∵△ABP∽△ECB，
∴ 
，
∵BP= 
，E为BP的中点，
∴BE= 
，
∴BC= 
，
过P作PH⊥PD交DE于H，
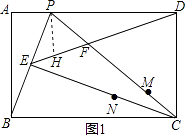
∴PD=BC﹣AP= 
，
∵∠BEC=∠ADC=90°，
∴P，E．C，D四点共圆，
∴∠PDH=∠PCE=∠BCE=∠ABP，
∴△APB∽△PHD，
∴ 
，
∴PH= 
，
∴ 
= 
；
②当k= 
时， 
= 
，
过F作FG⊥BC于G交CE于N，反向延长交AD于H，
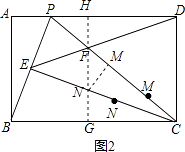
则FH⊥AD，过N作NM⊥PC于M，
∴NF+NM的最小值即为FG的长，
∴ 
，
∴FG= 
，
即NF+NM的最小值是 ．
【解析】（1）根据矩形的想知道的∠A=∠ABC=90°，由余角的性质得到∠APB=∠PBC，根据相似三角形的判定定理即可得到结论；（2）①根据相似三角形的性质得到 ，得到BP= ，过P作PH⊥PD交DE于H，推出P，E．C，D四点共圆，根据圆周角定理得到∠PDH=∠PCE=∠BCE=∠ABP，根据相似三角形的想知道的 ，即可得到结论；②把k= 代入 = ，过F作FG⊥BC于G交CE于N，反向延长交AD于H，则FH⊥AD，过N作NM⊥PC于M，根据线段公理得到NF+NM的最小值即为FG的长，即可得到结论．
【考点精析】解答此题的关键在于理解相似三角形的性质的相关知识，掌握对应角相等，对应边成比例的两个三角形叫做相似三角形．
