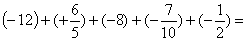题目内容
已知:如图,四边形 ABCD 中,AB⊥BC,AB=1,BC=2,CD=2,AD=3,求四边形 ABCD 的 面积.
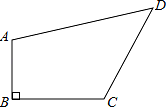
【考点】勾股定理的逆定理;勾股定理.
【分析】先根据勾股定理求出 AC 的长度,再根据勾股定理的逆定理判断出△ACD 的形状,再利用 三角形的面积公式求解即可.
【解答】解:连接 AC.
∵∠ABC=90°,AB=1,BC=2,
∴AC=  =
=  ,
,
在△ACD 中,AC2+CD2=5+4=9=AD2,
∴△ACD 是直角三角形,

 ∴S 四边形 ABCD= AB•BC+ AC•CD,
∴S 四边形 ABCD= AB•BC+ AC•CD,

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
为了鼓励居民节约用水,万源市民生给排水公司对居民生活用水按阶梯式水价计费,下表是我 市居民“一户一表”生活用水阶梯式计费价格表的一部分信息:
| 自来水销售价格 | 污水处理价格 | |
| 每户每月用水量 | 单价:元/吨 | 单价:元/吨 |
| 12 吨以下(含 12 吨) | a | 0.15 |
| 超过 12 吨不超过 18 吨的部分 | b | |
| 超过 18 吨的部分 | 4.5 |
[说明:①每户产生的污水量等于该户的用水量;②水费=自来水费+污水处理费
(1)已知小李家 2013 年 4 月份用水量 16 吨,交水费 45.2 元;5 月份用水量 14 吨,交水费 37.9 元.求 表中 a、b 的值.
设小李家每月用水量为 x 吨,交水费 y 元,求 y(元)与 x(吨)的函数关系式,并指出自变量 x 的 取值范围.
 ﹣(﹣25)×
﹣(﹣25)× 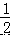 +(﹣
+(﹣ 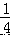 )×25.
)×25.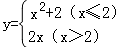 则当函数值 y=8 时,自变量 x 的值等于
则当函数值 y=8 时,自变量 x 的值等于 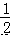 )+(x+
)+(x+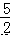 ),其中 x=﹣
),其中 x=﹣ .
.