题目内容
 如图,已知点A(1,1),B(3,2),且P为x轴上一动点,则△ABP周长的最小值为________.
如图,已知点A(1,1),B(3,2),且P为x轴上一动点,则△ABP周长的最小值为________.
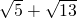
分析:本题需先根据已知条件求出AB的长,再根据P为x轴上一动点,确定出P点的位置,即可求出BP+AP的长,最后即可求出△ABP周长的最小值.
解答:
 解:做点B关于X轴的对称点B′,连接AB′,当点P运动到AB′与X轴的交点时
解:做点B关于X轴的对称点B′,连接AB′,当点P运动到AB′与X轴的交点时△ABP周长的最小值.
∵A(1,1),B(3,2),
∴AB=
 =
=
又∵P为x轴上一动点,
当求△ABP周长的最小值时,
∴AB′=
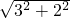 =
=
∴△ABP周长的最小值为:AB+AB′=
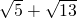
故答案为:
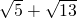
点评:本题主要考查了轴对称-最短路线问题,在解题要结合图形再与各个知识点相结合,找出点P所在的位置是本题的关键.

练习册系列答案
相关题目
 如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10cm.图中阴影部分的面积为( )
如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10cm.图中阴影部分的面积为( )A、
| ||||
B、
| ||||
C、2
| ||||
D、4
|
 16、如图,已知点D是∠ABC的平分线上一点,点P在BD上,PA⊥AB,PC⊥BC,垂足分别为A,C、下列结论错误的是( )
16、如图,已知点D是∠ABC的平分线上一点,点P在BD上,PA⊥AB,PC⊥BC,垂足分别为A,C、下列结论错误的是( )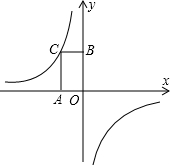 如图,已知点C为反比例函数y=-
如图,已知点C为反比例函数y=- 如图,已知点D为△ABC中AC边上一点,且AD:DC=3;4,设
如图,已知点D为△ABC中AC边上一点,且AD:DC=3;4,设 如图,已知点C为AB上一点,AC=12cm,CB=
如图,已知点C为AB上一点,AC=12cm,CB=