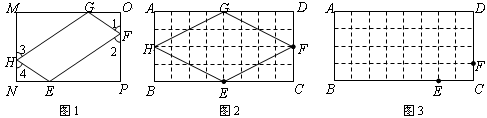
题目内容
如图1,矩形MNPQ中,点E,F,G,H分别在NP,PQ,QM,MN上,若 ,则称四边形EFGH为矩形MNPQ的反射四边形.图2,图3,图4中,四边形ABCD为矩形,且
,则称四边形EFGH为矩形MNPQ的反射四边形.图2,图3,图4中,四边形ABCD为矩形,且 ,
, .
.
理解与作图:
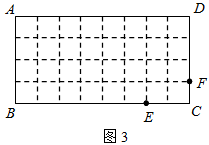
(1)在图2,图3中,点E,F分别在BC,CD边上,试利用正方形网格在图上作出矩形ABCD的反射四边形EFGH.
计算与猜想:
(2)求图2,图3中反射四边形EFGH的周长,并猜想矩形ABCD的反射四边形的周长是否为定值?
启发与证明:
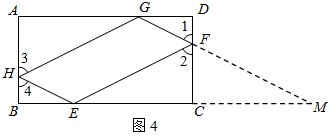
(3)如图4,为了证明上述猜想,小华同学尝试延长GF交BC的延长线于M,试利用小华同学给我们的启发证明(2)中的猜想.

(1)作图如下:

(2)是;(3)见解析
【解析】
试题分析:(1)根据网格结构,作出相等的角即可得到反射四边形;
(2)图2中,利用勾股定理求出EF=FG=GH=HE的长度,然后即可得到周长,图3中利用勾股定理求出EF=GH,FG=HE的长度,然后求出周长,从而得到四边形EFGH的周长是定值;
(3)证法一:延长GH交CB的延长线于点N,再利用“角边角”证明Rt△FCE和Rt△FCM全等,根据全等三角形对应边相等可得EF=MF,EC=MC,同理求出NH=EH,NB=EB,从而得到MN=2BC,再证明GM=GN,过点G作GK⊥BC于K,根据等腰三角形三线合一的性质求出MK= MN=8,再利用勾股定理求出GM的长度,然后即可求出四边形EFGH的周长;
MN=8,再利用勾股定理求出GM的长度,然后即可求出四边形EFGH的周长;
证法二:利用“角边角”证明Rt△FCE和Rt△FCM全等,根据全等三角形对应边相等可得EF=MF,EC=MC,再根据角的关系推出∠M=∠HEB,根据同位角相等,两直线平行可得HE∥GF,同理可证GH∥EF,所以四边形EFGH是平行四边形,过点G作GK⊥BC于K,根据边的关系推出MK=BC,再利用勾股定理列式求出GM的长度,然后即可求出四边形EFGH的周长.
(1)作图如下:

(2)在图2中, ,
,
∴四边形EFGH的周长为 .
.
在图3中, ,
, .
.
∴四边形EFGH的周长为 .
.
猜想:矩形ABCD的反射四边形的周长为定值.
(3)证法一:延长GH交CB的延长线于点N.

∵ ,
, ,
,
∴ .
.
而 ,
,
∴Rt△FCE≌Rt△FCM.
∴ ,
, .
.
同理: ,
, .
.
∴ .
.
∵ ,
, ,
,
∴ .
.
∴ .
.
过点G作GK⊥BC于K,则 .
.
∴ .
.
∴四边形EFGH的周长为 .
.
证法二:∵ ,
, ,
,
∴ .
.
而 ,
,
∴Rt△FCE≌Rt△FCM.
∴ ,
, .
.
∵ ,
, ,
,
而 ,
,
∴ .
.
∴HE∥GF.
同理:GH∥EF.
∴四边形EFGH是平行四边形.
∴ .
.
而 ,
,
∴Rt△FDG≌Rt△HBE.
∴ .
.
过点G作GK⊥BC于K,则 .
.
∴ .
.
∴四边形EFGH的周长为 .
.
考点:本题考查了应用与设计作图,全等三角形的判定与性质,勾股定理的应用,矩形的性质,
点评:解答本题的关键读懂题意,准确理解“反射四边形EFGH”特征.

 阅读快车系列答案
阅读快车系列答案
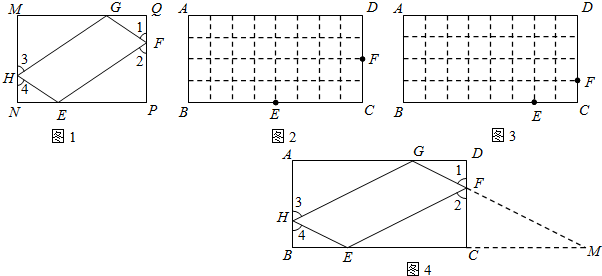
 如图,在矩形MNPQ中,MN=6,PN=4,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y,
如图,在矩形MNPQ中,MN=6,PN=4,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y,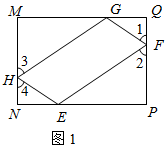
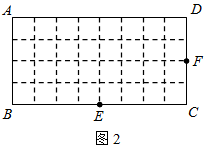
 ,则称四边形EFGH为矩形MNPQ的反射四边形.在图2、图3中,四边形ABCD为矩形,且
,则称四边形EFGH为矩形MNPQ的反射四边形.在图2、图3中,四边形ABCD为矩形,且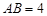 ,
,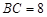 .
.