题目内容
 如图,点A、B、O是正方形网格上的三个格点,⊙O的半径为OA,点P是优弧
如图,点A、B、O是正方形网格上的三个格点,⊙O的半径为OA,点P是优弧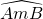 上的一点,则tan∠APB=________.
上的一点,则tan∠APB=________.
1
分析:由点A、B、O是正方形网格上的三个格点,⊙O的半径为OA,易得∠AOB=90°,又由圆周角定理,可求得∠APB的度数,继而求得答案.
解答:∵点A、B、O是正方形网格上的三个格点,
∴∠AOB=90°,
∴∠APB= ∠AOB=45°,
∠AOB=45°,
∴tan∠APB=1.
故答案为:1.
点评:此题考查了圆周角定理与锐角三角函数.此题难度不大,注意掌握数形结合思想的应用.
分析:由点A、B、O是正方形网格上的三个格点,⊙O的半径为OA,易得∠AOB=90°,又由圆周角定理,可求得∠APB的度数,继而求得答案.
解答:∵点A、B、O是正方形网格上的三个格点,
∴∠AOB=90°,
∴∠APB=
 ∠AOB=45°,
∠AOB=45°,∴tan∠APB=1.
故答案为:1.
点评:此题考查了圆周角定理与锐角三角函数.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
 8、如图,点A,B,C是⊙O上的三点,∠BAC=40°,则∠OBC的度数是( )
8、如图,点A,B,C是⊙O上的三点,∠BAC=40°,则∠OBC的度数是( ) 如图,点A、B、C是⊙O上的三点,若∠BOC=50°,则∠A的度数为
如图,点A、B、C是⊙O上的三点,若∠BOC=50°,则∠A的度数为
 如图,点A、B、C是⊙O上的三点,∠BAC=40°,则∠BOC的度数是( )
如图,点A、B、C是⊙O上的三点,∠BAC=40°,则∠BOC的度数是( ) 如图,点A、B、C是圆O上的三点,OB⊥AC,∠BAC=40°,则∠OCA=( )
如图,点A、B、C是圆O上的三点,OB⊥AC,∠BAC=40°,则∠OCA=( )