题目内容
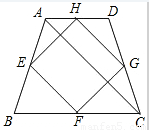
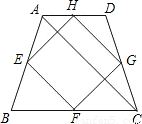
 某花木场有一块形如等腰梯形ABCD的空地(如图),各边的中点分别是E、F、G、H,测量得对角线AC=10m,现想用篱笆围成四边形EFGH的场地,则篱笆的总长度是
某花木场有一块形如等腰梯形ABCD的空地(如图),各边的中点分别是E、F、G、H,测量得对角线AC=10m,现想用篱笆围成四边形EFGH的场地,则篱笆的总长度是分析:根据三角形中位线定理和等腰梯形的对角线相等可证明篱笆的形状为菱形,且边长等于等腰梯形的对角线的一半,即可求得篱笆总长度.
解答: 解:连接BD.
解:连接BD.
根据三角形中位线定理,得
EF=HG=
AC=5,EH=FG=
BD.
∵四边形ABCD是等腰梯形,
∴AC=BD.
∴EF=FG=GH=HE=5.
∴需篱笆总长度是EF+HG+EH+GF=2AC=2×10=20(米).
故答案为:20.
 解:连接BD.
解:连接BD.根据三角形中位线定理,得
EF=HG=
| 1 |
| 2 |
| 1 |
| 2 |
∵四边形ABCD是等腰梯形,
∴AC=BD.
∴EF=FG=GH=HE=5.
∴需篱笆总长度是EF+HG+EH+GF=2AC=2×10=20(米).
故答案为:20.
点评:本题考查了等腰梯形的性质及三角形的中位线定理,难度不大,但是要注意:顺次连接对角线相等的四边形各边中点所得四边形是菱形.

练习册系列答案
相关题目
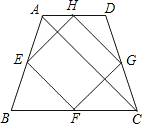 如图,某花木场有一块形如等腰梯形ABCD的空地,各边的中点分别是E,F,G,H,测量得对角线AC=10米,现想用篱笆围成四边形EFGH的场地,则需篱笆总长度是( )
如图,某花木场有一块形如等腰梯形ABCD的空地,各边的中点分别是E,F,G,H,测量得对角线AC=10米,现想用篱笆围成四边形EFGH的场地,则需篱笆总长度是( )| A、40米 | B、30米 | C、20米 | D、10米 |
 某花木场有一块形如等腰梯形ABCD的空地(如图),各边中点分别为E、F、G、H,测得对角线AC=5m,若用篱笆围成四边形EFGH的场地,则需篱笆总长度为
某花木场有一块形如等腰梯形ABCD的空地(如图),各边中点分别为E、F、G、H,测得对角线AC=5m,若用篱笆围成四边形EFGH的场地,则需篱笆总长度为