题目内容
【题目】如图,四边形OABC是平行四边形,点C在x轴上,反比例函数y= ![]() (x>0)的图象经过点A(5,12),且与边BC交于点D.若AB=BD,则点D的坐标为 .
(x>0)的图象经过点A(5,12),且与边BC交于点D.若AB=BD,则点D的坐标为 . 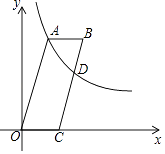
【答案】(8,![]() )
)
【解析】解:∵反比例函数y= ![]() (x>0)的图象经过点A(5,12),
(x>0)的图象经过点A(5,12),
∴k=12×5=60,
∴反比例函数的解析式为y= ![]() ,
,
设D(m, ![]() ),
),
由题可得OA的解析式为y= ![]() x,AO∥BC,
x,AO∥BC,
∴可设BC的解析式为y= ![]() x+b,
x+b,
把D(m, ![]() )代入,可得
)代入,可得 ![]() m+b=
m+b= ![]() ,
,
∴b= ![]() ﹣
﹣ ![]() m,
m,
∴BC的解析式为y= ![]() x+
x+ ![]() ﹣
﹣ ![]() m,
m,
令y=0,则x=m﹣ ![]() ,即OC=m﹣
,即OC=m﹣ ![]() ,
,
∴平行四边形ABCO中,AB=m﹣ ![]() ,
,
如图所示,过D作DE⊥AB于E,过A作AF⊥OC于F,则△DEB∽△AFO,
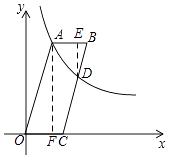
∴ ![]() =
= ![]() ,而AF=12,DE=12﹣
,而AF=12,DE=12﹣ ![]() ,OA=
,OA= ![]() =13,
=13,
∴DB=13﹣ ![]() ,
,
∵AB=DB,
∴m﹣ ![]() =13﹣
=13﹣ ![]() ,
,
解得m1=5,m2=8,
又∵D在A的右侧,即m>5,
∴m=8,
∴D的坐标为(8, ![]() ).
).
所以答案是:(8, ![]() ).
).
【考点精析】通过灵活运用平行四边形的性质,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分即可以解答此题.

练习册系列答案
相关题目
【题目】某学习小组在研究函数y= ![]() x3﹣2x的图象与性质时,已列表、描点并画出了图象的一部分.
x3﹣2x的图象与性质时,已列表、描点并画出了图象的一部分.
x | … | ﹣4 | ﹣3.5 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 3.5 | 4 | … |
y | … | ﹣ | ﹣ |
|
|
| 0 | ﹣ | ﹣ | ﹣ |
|
| … |
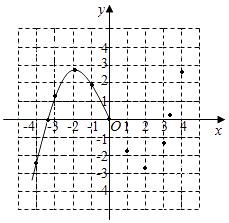
(1)请补全函数图象;
(2)方程 ![]() x3﹣2x=﹣2实数根的个数为;
x3﹣2x=﹣2实数根的个数为;
(3)观察图象,写出该函数的两条性质.



