Question

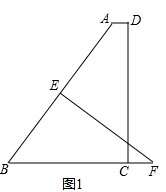
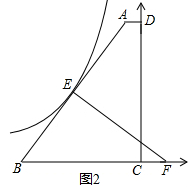
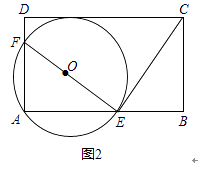
【题目】如图，点E，C在BF上，，，．

求证：；

若AC交DE于M，且，，将线段CE绕点C顺时针旋转，使点E旋转到AB上的G处，求旋转角的度数．

Answer 1

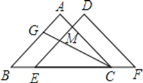
【答案】(1)见解析;(2)15°.

【解析】

（1）通过证明△ABC≌△DEF即可得出AB=DE．

（2）要求角的度数就要解直角三角形，根据特殊角的三角函数值来计算．

（1）证明：∵BE=FC，

∴BC=EF，

又∵∠ABC=∠DEF，∠A=∠D，

∴△ABC≌△DEF，

∴AB=DE．

（2）解：∵∠DEF=∠B=45°，

∴DE∥AB，

∴∠CME=∠A=90°，

∴AC=AB= ，MC=ME= ，

∴在Rt△MEC中，EC===2，

∴CG=CE=2，

在Rt△CAG中，cos∠ACG==，

∴∠ACG=30°，

∴∠ECG=∠ACB-∠ACG=45°-30°=15°．