题目内容
【题目】恩施州绿色、富硒产品和特色农产品在国际市场上颇具竞争力,其中香菇远销日本和韩国等地.上市时,外商李经理按市场价格10元/千克在我州收购了2000千克香菇存放入冷库中.据预测,香菇的市场价格每天每千克将上涨0.5元,但冷库存放这批香菇时每天需要支出各种费用合计340元,而且香菇在冷库中最多保存110天,同时,平均每天有6千克的香菇损坏不能出售.
(1)若存放x天后,将这批香菇一次性出售,设这批香菇的销售总金额为y元,试写出y与x之间的函数关系式.
(2)李经理想获得利润22500元,需将这批香菇存放多少天后出售?(利润=销售总金额﹣收购成本﹣各种费用)
(3)李经理将这批香菇存放多少天后出售可获得最大利润?最大利润是多少?
【答案】(1)y==﹣3x2+940x+20000(1≤x≤110,且x为整数);
(2)李经理 想获得利润22500元,需将这批香菇存放多少天后出售?(利润=销售总金额﹣收购成本﹣各种费用)
(3)李经理将这批香菇存放多少天后出售可获得最大利润?最大利润是多少?
【解析】试题分析:(1)根据等量关系“销售总金额=(市场价格+0.5×存放天数)×(原购入量-6×存放天数)”列出函数关系式;
(2)按照等量关系“利润=销售总金额-收购成本-各种费用”列出函数方程求解即可;
(3)根据等量关系“利润=销售总金额-收购成本-各种费用”列出函数关系式并求最大值.
试题解析:(1)由题意y与x之间的函数关系式为y=(10+0.5x)(20006x),
![]() (
(![]() ,且x为整数);
,且x为整数);
(2)由题意得:
![]() ,
,
解方程得: ![]() (不合题意,舍去)
(不合题意,舍去)
李经理想获得利润22500元需将这批香菇存放50天后出售;
(3)设利润为w,由题意得
![]()
∵a=3<0,
∴抛物线开口方向向下,
∴x=100时,w最大=30000
100天<110天
∴存放100天后出售这批香菇可获得最大利润30000元.

【题目】观察如图图形,把一个三角形分别连接其三边中点,构成4个小三角形,挖去中间的一个小三角形(如图1),对剩下的三个小三角形再分别重复以上做法,……,据此解答下面的问题
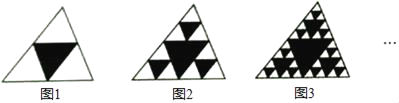
(1)填写下表:
图形 | 挖去三角形的个数 |
图形1 | 1 |
图形2 | 1+3 |
图形3 | 1+3+9 |
图形4 |
|
(2)根据这个规律,求图n中挖去三角形的个数wn;(用含n的代数式表示)
(3)若图n+1中挖去三角形的个数为wn+1,求wn+1﹣Wn